Overview

What is cuDecomp?

cuDecomp is a library for managing 1D (slab) and 2D (pencil) parallel decompositions of 3D Cartesian spatial domains on NVIDIA GPUs, with routines to perform global transpositions and halo communication. The library is inspired by the 2DECOMP&FFT Fortran library , a popular decomposition library for numerical simulation codes, with a similar set of available transposition routines. While 2DECOMP&FFT and similar libraries in the past have been written to target CPU systems, this library is designed for GPU systems, leveraging CUDA-aware MPI and additional communication libraries optimized for GPUs, like the NVIDIA Collective Communication Library (NCCL) and NVIDIA OpenSHMEM Library (NVSHMEM).

It is typical for modern GPU systems to have a hierarchy of connections between peer GPUs with wide-ranging bandwidths, from fast P2P connections through NVLINK/NVSWITCH between GPUs within a single compute node, to relatively slower inter-node network connections via Infiniband or Ethernet. Multi-socket nodes can also introduce cross-socket CPU connections where direct NVLINK connections are not available between GPUs. As a user, it can be challenging to navigate these various topologies and choose an appropriate decomposition of the domain to optimize network performance for their workload. To add to this complexity, there are numerous communication libraries available for GPUs to choose from, with performance characteristics for GPUs varying based on these system topologies, scale, message sizes (and for MPI, the particular implementation used). To address this challenge, cuDecomp has a runtime autotuning feature that can sweep across possible domain decompositions and several communication backends using different communication libraries to find the option that minimizes either the transposition or halo communication time. For applications that require global transpositions (e.g., FFT-based solvers, ADI solvers), the time to transpose the domain is generally a large bottleneck, so minimizing this time is often key to ensuring good solver performance. Using autotuning, cuDecomp can assist users in maintaining high computational performance across problem sizes and clusters. See the autotuning section [link] for more information on this feature.

Decomposition Layout

cuDecomp can distribute 3D Cartesian domains with dimensions \([X, Y, Z]\), in column-major order, which we will call the global grid. The global grid is decomposed across \(N_{\text{GPU}}\) processes in a 2D process grid with dimensions \(P_{\text{row}} \times P_{\text{col}}\). The processes are logically grouped by column and row index into \(P_{\text{row}}\) row communicators and \(P_{\text{col}}\) column communicators. For consistency with MPI_Cart_* routines, the ranks are assigned in a row-major ordering (i.e. row communicators are composed of sequential ranks).

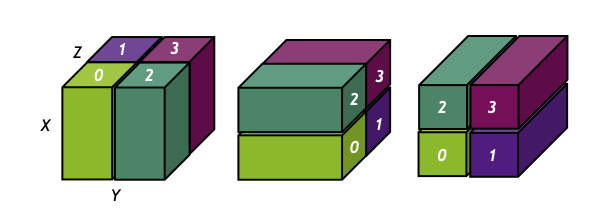
cuDecomp will distribute the global domain data so that each process is assigned a unique pencil of data, with three different pencil configurations corresponding to different transposed configurations of the global domain. The domain can be decomposed into \(X\)-axis aligned pencils (\(X\)-pencils), where the \(Y\) and \(Z\) dimensions are split across the process grid, \(Y\)-axis aligned pencils (\(Y\)-pencils), where the \(X\) and \(Z\) dimensions are split across the process grid, or \(Z\)-axis aligned pencils (\(Z\)-pencils), where the \(X\) and \(Y\) dimensions are split across the process grid. The shapes of these pencils are approximately:

\(X\)-pencils	\([X, \; Y/P_{\text{row}}, \; Z/P_{\text{col}}]\)
\(Y\)-pencils	\([X/P_{\text{row}}, \; Y, \; Z/P_{\text{col}}]\)
\(Z\)-pencils	\([X/P_{\text{row}}, \; Y/P_{\text{col}}, \; Z]\)

In the case where the global dimension is not evenly divisible by \(P_{\text{row}}\) or \(P_{\text{col}}\) in the formulas above, the remainder is distributed across the row or column ranks starting from the lowest indexed rank.

A simple illustration of the decomposition using a \(2 \times 2\) process grid is shown below. From left to right, the illustration shows the \(X\)-pencil, \(Y\)-pencil, and \(Z\)-pencil configurations, with associated rank assignments.