Mixed Precision Training¶
Increasing the size of a neural network typically improves accuracy but also increases the memory and compute requirements for training the model. We introduce methodology for training deep neural networks using half-precision floating point numbers, without losing model accuracy or having to modify hyperparameters. This nearly halves memory requirements and, on recent GPUs, speeds up arithmetic. …
DNN operations benchmarked with DeepBench on Volta GPU see 2-6x speedups compared to FP32 implementations if they are limited by memory or arithmetic bandwidth. Speedups are lower when operations are latency-limited.
—“Mixed Precision Training”, Micikevicius et al, ICLR, 2018
Prerequisites¶
Mixed precision training utilizes Tensor Cores introduced in NVIDIA Volta GPUs such as Titan V and Tesla V100. NVIDIA Volta GPUs are also available from AWS on p3.2xlarge, p3.8xlarge, p3.16xlarge instances .
For an optimal mixed precision performance we recommend using NVIDIA’s TensorFlow docker containers (version 18.03 and above) which can be obtained here: NVIDIA GPU cloud . Alternatively, you can build TensorFlow yourself with CUDA 9.1 and this PR included:
How to enable mixed precision¶
Enabling mixed precision with existing models in OpenSeq2Seq is simple:
change dtype parameter of model_params to “mixed”.
You might need to enable loss scaling: either statically, by setting
loss_scale parameter inside model_params to the desired number, or
you can use dynamic loss scaling by setting automatic_loss_scaling parameter
to “Backoff” or “LogMax”:
base_params = {
...
"dtype": "mixed",
# enabling static or dynamic loss scaling might improve model convergence
# "loss_scale": 10.0,
# "automatic_loss_scaling": "Backoff",
...
}
Implementation details¶
For mixed precision training we follow an algorithmic recipe from Micikevicius et al [1]. At a high level it can be summarized as follows:
- Maintain and update a float32 master copy of weights (using the float16 copy for forward and back propagation)
- Apply loss scaling while computing gradients
It is worth mentioning that (1)-(2) are not always necessary. However, this method has proven to be robust across a variety of bigger and more complex models.
Note that while (1) does mean a 50% increase in memory consumption for weights over a float32 version, in practice, the total memory consumption is often decreased. This is because activations, activation gradients, and other intermediate tensors can now be kept in float16. This is especially beneficial for models with a high degree of parameter sharing or reuse, such as recurrent models with many timesteps.
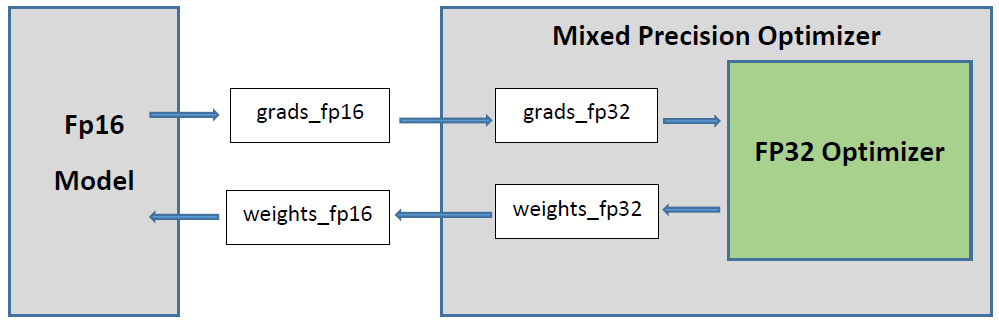
Optimizer¶
Our implementation is different from the one described in
NVIDIA documentation:
instead of a custom variable getter, we introduce a wrapper around standard
TensorFlow optimizers. The model is created with float16 data type, so all
variables and gradients are in float16 by default (except for the layers which
are explicitly redefined as float32; for example data layers or operations on
CPU). The wrapper then converts float16 gradients to float32 and submits them
to TensorFlow’s optimizer, which updates the master copy of weights. Updated
weights are converted back to float16, and used by the model in the next
iteration. The MixedPrecisionOptimizerWrapper
architecture is graphically illustrated below:
Regularizers¶
MixedPrecisionOptimizerWrapper
ensures that all float16 variables will have
a master copy in float32 and that their gradients will be cast to the full
precision before computing the weight update. While this is enough in most
situations, in some cases it is important to keep the gradient in float32 from
the beginning of the computation. One common case when this is necessary is
weight decay regularization. This regularization results in the following
addition to the usual gradients with respect to the loss:
\(\frac{\partial L}{\partial w} \mathrel{+}= 2\lambda w\),
where \(\lambda\) is usually on the order of
\(\left[10^{-5}, 10^{-3}\right]\).
Given that the weights are commonly initialized with small values, multiplying
them with weight decay coefficient $lambda$ can result in numerical underflow.
To overcome this problem we implemented the following design principles. First,
all regularizers should be defined on the variable creation level by passing
regularizer function as a regularizer parameter to the tf.get_variable
function or tf.layers objects (this is a recommended way to do it in
TensorFlow). Second, the regularizer function should be wrapped with
mp_regularizer_wrapper
function which will do two things. First, it
will add weights and the user-provided regularization function to the TensorFlow
collection. And second, it will disable the underlying regularization function
by returning None (only if the weights are in float16, otherwise it will not
introduce any additional behavior). The created collection will later be
retrieved by MixedPrecisionOptimizerWrapper and the corresponding
functions will be applied to the float32 copy of the weights ensuring that their
gradients always stay in the full precision. Since this regularization will not
be a part of the loss computation graph, we explicitly call tf.gradients
and add the result to the gradients passed in the compute_gradients
function of the optimizer.
Automatic Loss Scaling¶
The mixed precision training approach suggests that the user set a loss scale hyperparameter to adjust the dynamic range of backpropagation to match the dynamic range of float16. OpenSeq2Seq implements an extension to the mixed precision recipe that we call automatic loss scaling. The optimizer inspects the parameter gradients at each iteration and uses their values to select the loss scale for the next iteration. As a result, the user does not have to select the loss-scale value manually. Concretely, OpenSeq2Seq has support for two automatic loss scaling algorithms, Backoff and LogNormal scaling.
- Backoff scaling begins with a large loss scale and checks for overflow in the parameter gradients at the end of each iteration. Whenever there is an overflow, the loss scale decreases by a constant factor (default is 2) and the optimizer will skip the update. Furthermore, if there has been no overflow for a period of time, the loss scale increases by a constant factor (defaults are 2000 iterations and 2, respectively). These two rules together ensure both that the loss scale is as large as possible and also that it can adjust to shifting dynamic range during training.
- LogNormal scaling uses gradient statistics, rather than the presence of overflow, to set the loss scale. It keeps a running estimate of the mean and variance of the inter-iteration maximum absolute value of the parameter gradients. It models the inter-iteration maximum as log-normally distributed (hence the name), and then chooses the loss scale for the next iteration s.t. the probability of the maximum overflowing float16 is less than some constant (default is 0.001). In the rare event of an overflow, the optimizer skips the update.
| [1] | Paulius Micikevicius, Sharan Narang, Jonah Alben, Gregory Diamos, Erich Elsen, David Garcia, Boris Ginsburg, Michael Houston, Oleksii Kuchaev, Ganesh Venkatesh, and others. Mixed precision training. arXiv preprint arXiv:1710.03740, 2017. |