Hybrid Quantum Neural Networks¶
The example below highlights a hybrid quantum neural network workflow with CUDA-Q and PyTorch where both layers can GPU accelerated to maximise performance.
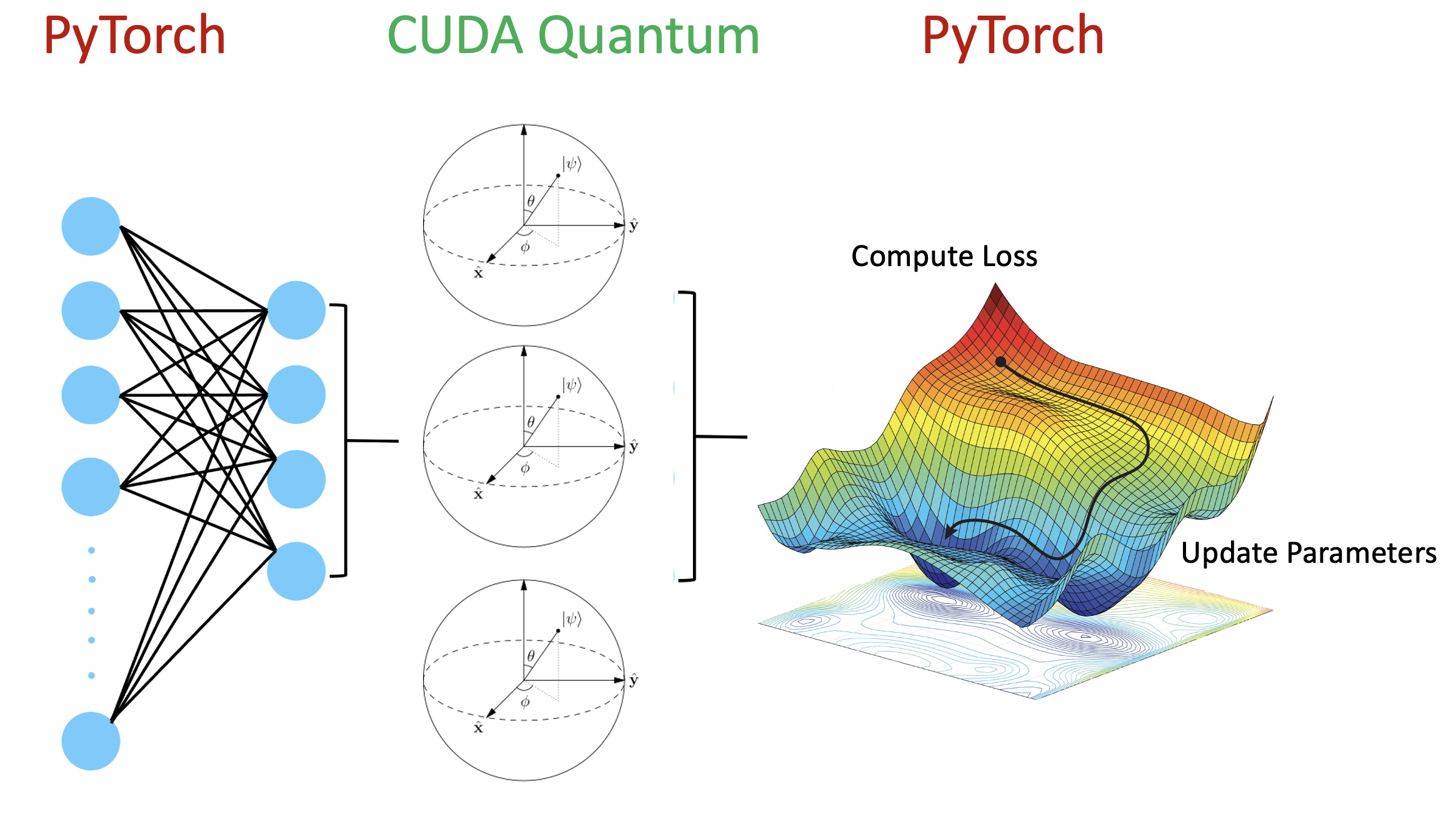
We perform binary classification on the MNIST dataset where data flows through the neural network architecture to the quantum circuit whose output is used to classify hand written digits.
[1]:
# Import the relevant packages.
!pip install matplotlib==3.8.4
!pip install torch==2.2.2
!pip install torchvision==0.17.0
!pip install scikit-learn==1.4.2
import cudaq
from cudaq import spin
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.autograd import Function
from torchvision import datasets, transforms
import torch.optim as optim
import torch.nn as nn
import torchvision
from sklearn.model_selection import train_test_split
torch.manual_seed(22)
cudaq.set_random_seed(44)
[2]:
# Set CUDAQ and PyTorch to run on either CPU or GPU.
device = torch.device('cpu')
cudaq.set_target("qpp-cpu")
# cudaq.set_target("nvidia")
# device = torch.device("cuda:0")
[3]:
def prepare_data(target_digits, sample_count, test_size):
"""Load and prepare the MNIST dataset to be used
Args:
target_digits (list): digits to perform classification of
sample_count (int): total number of images to be used
test_size (float): percentage of sample_count to be used as test set, the remainder is the training set
Returns:
dataset in train, test format with targets
"""
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.1307), (0.3081))])
dataset = datasets.MNIST("./data",
train=True,
download=True,
transform=transform)
# Filter out the required labels.
idx = (dataset.targets == target_digits[0]) | (dataset.targets
== target_digits[1])
dataset.data = dataset.data[idx]
dataset.targets = dataset.targets[idx]
# Select a subset based on number of datapoints specified by sample_count.
subset_indices = torch.randperm(dataset.data.size(0))[:sample_count]
x = dataset.data[subset_indices].float().unsqueeze(1).to(device)
y = dataset.targets[subset_indices].to(device).float().to(device)
# Relabel the targets as a 0 or a 1.
y = torch.where(y == min(target_digits), 0.0, 1.0)
x_train, x_test, y_train, y_test = train_test_split(x,
y,
test_size=test_size /
100,
shuffle=True,
random_state=42)
return x_train, x_test, y_train, y_test
[4]:
# Classical parameters.
sample_count = 1000 # Total number of images to use.
target_digits = [5, 6] # Hand written digits to classify.
test_size = 30 # Percentage of dataset to be used for testing.
classification_threshold = 0.5 # Classification boundary used to measure accuracy.
epochs = 1000 # Number of epochs to train for.
# Quantum parmeters.
qubit_count = 1
hamiltonian = spin.z(0) # Measurement operator.
shift = torch.tensor(torch.pi / 2) # Magnitude of parameter shift.
[5]:
x_train, x_test, y_train, y_test = prepare_data(target_digits, sample_count,
test_size)
[6]:
# Plot some images from the training set to visualise.
grid_img = torchvision.utils.make_grid(x_train[:10],
nrow=5,
padding=3,
normalize=True)
plt.imshow(grid_img.permute(1, 2, 0))
plt.axis('off')
plt.show()
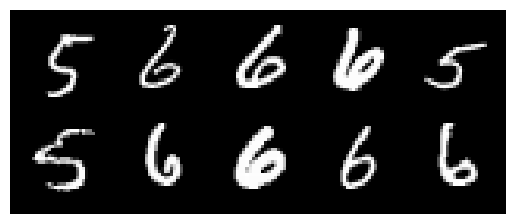
[7]:
class QuantumFunction(Function):
"""Allows the quantum circuit to input data, output expectation values
and calculate gradients of variational parameters via finite difference"""
def __init__(self, qubit_count: int, hamiltonian: cudaq.SpinOperator):
"""Define the quantum circuit in CUDA Quantum"""
@cudaq.kernel
def kernel(qubit_count: int, thetas: np.ndarray):
qubits = cudaq.qvector(qubit_count)
ry(thetas[0], qubits[0])
rx(thetas[1], qubits[0])
self.kernel = kernel
self.qubit_count = qubit_count
self.hamiltonian = hamiltonian
def run(self, theta_vals: torch.tensor) -> torch.tensor:
"""Excetute the quantum circuit to output an expectation value"""
#If running on GPU, thetas is a torch.tensor that will live on GPU memory. The observe function calls a .tolist() method on inputs which moves thetas from GPU to CPU.
qubit_count = [self.qubit_count for _ in range(theta_vals.shape[0])]
results = cudaq.observe(self.kernel, self.hamiltonian, qubit_count,
theta_vals)
exp_vals = [results[i].expectation() for i in range(len(results))]
exp_vals = torch.Tensor(exp_vals).to(device)
return exp_vals
@staticmethod
def forward(ctx, thetas: torch.tensor, quantum_circuit,
shift) -> torch.tensor:
# Save shift and quantum_circuit in context to use in backward.
ctx.shift = shift
ctx.quantum_circuit = quantum_circuit
# Calculate expectation value.
exp_vals = ctx.quantum_circuit.run(thetas).reshape(-1, 1)
ctx.save_for_backward(thetas, exp_vals)
return exp_vals
@staticmethod
def backward(ctx, grad_output):
"""Backward pass computation via finite difference"""
thetas, _ = ctx.saved_tensors
gradients = torch.zeros(thetas.shape, device=device)
for i in range(thetas.shape[1]):
thetas_plus = thetas.clone()
thetas_plus[:, i] += ctx.shift
exp_vals_plus = ctx.quantum_circuit.run(thetas_plus)
thetas_minus = thetas.clone()
thetas_minus[:, i] -= ctx.shift
exp_vals_minus = ctx.quantum_circuit.run(thetas_minus)
gradients[:, i] = (exp_vals_plus - exp_vals_minus) / (2 * ctx.shift)
gradients = torch.mul(grad_output, gradients)
return gradients, None, None
[8]:
class QuantumLayer(nn.Module):
"""Encapsulates a quantum circuit into a quantum layer adhering PyTorch convention"""
def __init__(self, qubit_count: int, hamiltonian, shift: torch.tensor):
super(QuantumLayer, self).__init__()
self.quantum_circuit = QuantumFunction(qubit_count, hamiltonian)
self.shift = shift
def forward(self, input):
result = QuantumFunction.apply(input, self.quantum_circuit, self.shift)
return result
[9]:
class Hyrbid_QNN(nn.Module):
"""Structure of the hybrid neural network with classical fully connected layers and quantum layers"""
def __init__(self):
super(Hyrbid_QNN, self).__init__()
self.fc1 = nn.Linear(28 * 28, 256)
self.fc2 = nn.Linear(256, 128)
self.dropout = nn.Dropout(0.25)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 32)
self.fc5 = nn.Linear(32, 2)
self.dropout = nn.Dropout(0.25)
# The 2 outputs from PyTorch fc5 layer feed into the 2 variational gates in the quantum circuit.
self.quantum = QuantumLayer(qubit_count, hamiltonian, shift)
def forward(self, x):
x = x.view(-1, 28 * 28) # Turns images into vectors.
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = self.dropout(x)
x = torch.relu(self.fc3(x))
x = torch.relu(self.fc4(x))
x = torch.relu(self.fc5(x))
x = self.dropout(x)
# Quantum circuit outputs an expectation value which is fed into the sigmoid activation function to perform classification.
x = torch.sigmoid(self.quantum(x))
return x.view(-1)
[10]:
def accuracy_score(y, y_hat):
return sum((y == (y_hat >= classification_threshold))) / len(y)
[11]:
hybrid_model = Hyrbid_QNN().to(device)
optimizer = optim.Adadelta(hybrid_model.parameters(),
lr=0.001,
weight_decay=0.8)
loss_function = nn.BCELoss().to(device)
training_cost = []
testing_cost = []
training_accuracy = []
testing_accuracy = []
hybrid_model.train()
for epoch in range(epochs):
optimizer.zero_grad()
y_hat_train = hybrid_model(x_train).to(device)
train_cost = loss_function(y_hat_train, y_train).to(device)
train_cost.backward()
optimizer.step()
training_accuracy.append(accuracy_score(y_train, y_hat_train))
training_cost.append(train_cost.item())
hybrid_model.eval()
with torch.no_grad():
y_hat_test = hybrid_model(x_test).to(device)
test_cost = loss_function(y_hat_test, y_test).to(device)
testing_accuracy.append(accuracy_score(y_test, y_hat_test))
testing_cost.append(test_cost.item())
[12]:
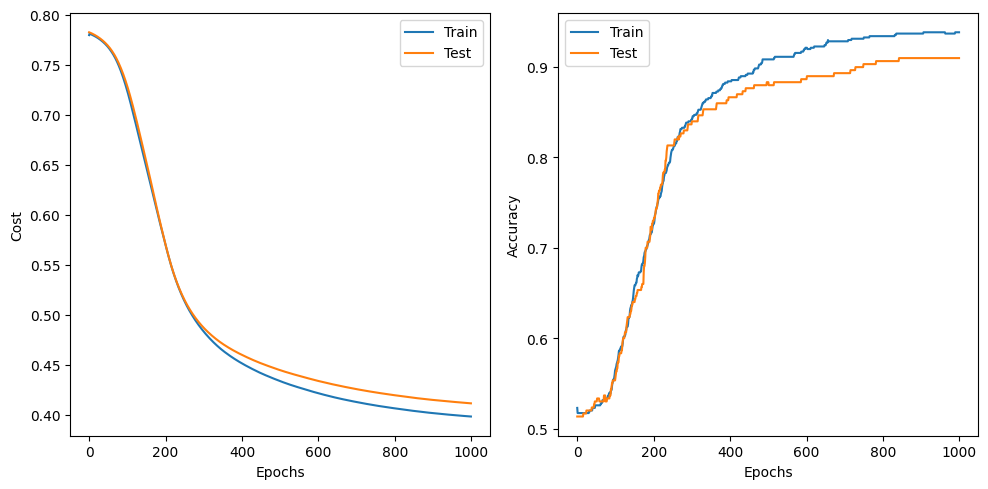
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(training_cost, label='Train')
plt.plot(testing_cost, label='Test')
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(training_accuracy, label='Train')
plt.plot(testing_accuracy, label='Test')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.tight_layout()
plt.show()
[13]:
print(cudaq.__version__)
CUDA-Q Version latest (https://github.com/NVIDIA/cuda-quantum a726804916fd397408cbf595ce6fe5f33dcd8b4c)