Variational Quantum Eigensolver

A common application of the Variational Quantum Eigensolver (VQE) algorithm is to compute the ground state energy of a molecular system. The code below demonstrates how to perform classical preprocessing for a \(H_2\) molecule (i.e. obtain the integrals from a Hartree-Fock computation to build the molecular Hamiltonian), prepare the initial Hartree-Fock state on the quantum register, add the parameterized UCCSD ansatz to the kernel, and select the COBYLA optimizer. We are then ready to call cudaq:vqe to estimate the minimum energy of the system.

!pip install openfermionpyscf==0.5 matplotlib==3.8.4 scipy==1.13.0

import cudaq
import matplotlib.pyplot as plt
from scipy.optimize import minimize
import numpy as np

# Single precision
cudaq.set_target("nvidia")
# Double precision
#cudaq.set_target("nvidia-fp64")

The problem of interest here is a chain of hydrogen atoms seperated along the z-axis at a fixed interval called the bond distance.

The interatomic electrostatic forces due to the electrons and protons and the shielding by the neutrons creates a chemical system whose energy can be minimised to find a stable configuration.

Let us first begin by defining the molecule and other metadata about the problem.

# Number of hydrogen atoms.
hydrogen_count = 2

# Distance between the atoms in Angstroms.
bond_distance = 0.7474

# Define a linear chain of Hydrogen atoms
geometry = [('H', (0, 0, i * bond_distance)) for i in range(hydrogen_count)]

hamiltonian, data = cudaq.chemistry.create_molecular_hamiltonian(
    geometry, 'sto-3g', 1, 0)

electron_count = data.n_electrons
qubit_count = 2 * data.n_orbitals

We now generate a Unitary Coupled-Cluster Singles and Doubles (UCCSD) ansatz from the template provided by CUDA-Q.

@cudaq.kernel
def kernel(thetas: list[float]):

    qubits = cudaq.qvector(qubit_count)

    for i in range(electron_count):
        x(qubits[i])

    cudaq.kernels.uccsd(qubits, thetas, electron_count, qubit_count)


parameter_count = cudaq.kernels.uccsd_num_parameters(electron_count,
                                                     qubit_count)

Using CUDA-Q Optimizers

We use the builtin optimizers within CUDA-Q for the minimization procedure.

optimizer = cudaq.optimizers.COBYLA()

energy, parameters = cudaq.vqe(kernel,
                               hamiltonian,
                               optimizer,
                               parameter_count=parameter_count)

print(energy)

-1.1371744305855906

Integration with Third-Party Optimizers

We can also integrate popular libraries like scipy with CUDA-Q.

# Define a function to minimize
def cost(theta):

    exp_val = cudaq.observe(kernel, hamiltonian, theta).expectation()

    return exp_val


exp_vals = []


def callback(xk):
    exp_vals.append(cost(xk))


# Initial variational parameters.
np.random.seed(42)
x0 = np.random.normal(0, np.pi, parameter_count)

# Use the scipy optimizer to minimize the function of interest
result = minimize(cost,
                  x0,
                  method='COBYLA',
                  callback=callback,
                  options={'maxiter': 40})

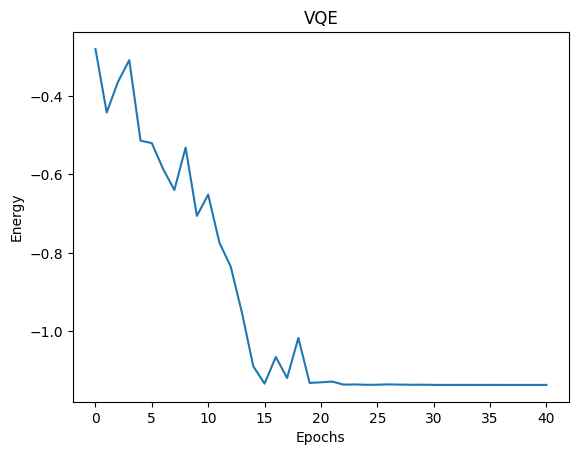
plt.plot(exp_vals)
plt.xlabel('Epochs')
plt.ylabel('Energy')
plt.title('VQE')
plt.show()