Sparse Tensor Networks¶
Sparse Tensor¶
In traditional speech, text, or image data, features are extracted densely. Thus, the most common representations used for these data are vectors, matrices, and tensors. However, for 3-dimensional scans or even higher-dimensional spaces, such dense representations are inefficient as effective information occupy only a small fraction of the space. Instead, we can only save information on the non-empty region of the space similar to how we save information on a sparse matrix. This representation is an N-dimensional extension of a sparse matrix; thus it is known as a sparse tensor.
In Minkowski Engine, we adopt the sparse tensor as the basic data
representation and the class is provided as
MinkowskiEngine.SparseTensor. Fore more information on sparse tensors
please refer to the terminology page.
Sparse Tensor Network¶
Compressing a neural network to speedup inference and minimize memory footprint has been studied widely. One of the popular techniques for model compression is pruning the weights in a convnet, is also known as a sparse convolutional networks [1]. Such parameter-space sparsity used for model compression still operates on dense tensors and all intermediate activations are also dense tensors.
However, in this work, we focus on spatially sparse data, in particular, spatially sparse high-dimensional inputs and convolutional networks for sparse tensors [2]. We can also represent these data as sparse tensors, and are commonplace in high-dimensional problems such as 3D perception, registration, and statistical data. We define neural networks specialized for these inputs sparse tensor networks and these sparse tensor networks processes and generates sparse tensors [4]. To construct a sparse tensor network, we build all standard neural network layers such as MLPs, non-linearities, convolution, normalizations, pooling operations as the same way we define on a dense tensor and implemented in the Minkowski Engine.
Generalized Convolution¶
The convolution is a fundamental operation in many fields. In image perception, convolutions have been the crux of achieving the state-of-the-art performance in many tasks and is proven to be the most crucial operation in AI, and computer vision research. In this work, we adopt the convolution on a sparse tensor [2] and propose the generalized convolution on a sparse tensor. The generalized convolution incorporates all discrete convolutions as special cases. We use the generalized convolution not only on the 3D spatial axes, but on any arbitrary dimensions, or also on the temporal axis, which is proven to be more effective than recurrent neural networks (RNN) in some applications.
Specifically, we generalize convolution for generic input and output coordinates, and for arbitrary kernel shapes. It allows extending a sparse tensor network to extremely high-dimensional spaces and dynamically generate coordinates for generative tasks. Also, the generalized convolution encompasses not only all sparse convolutions but also the conventional dense convolutions. We list some of characteristics and applications of generalized convolution below.
Sparse tensors for convolution kernels allow high-dimensional convolutions with specialized kernels [3]
Arbitrary input coordinates generalized convolution encompasses all discrete convolutions
Arbitrary output coordinates allows dynamic coordinate generation and generative networks [reconstruction and completion networks]
Let \(x^{\text{in}}_\mathbf{u} \in \mathbb{R}^{N^\text{in}}\) be an \(N^\text{in}\)-dimensional input feature vector in a \(D\)-dimensional space at \(\mathbf{u} \in \mathbb{R}^D\) (a D-dimensional coordinate), and convolution kernel weights be \(\mathbf{W} \in \mathbb{R}^{K^D \times N^\text{out} \times N^\text{in}}\). We break down the weights into spatial weights with \(K^D\) matrices of size \(N^\text{out} \times N^\text{in}\) as \(W_\mathbf{i}\) for \(|\{\mathbf{i}\}_\mathbf{i}| = K^D\). Then, the conventional dense convolution in D-dimension is
where \(\mathcal{V}^D(K)\) is the list of offsets in \(D\)-dimensional hypercube centered at the origin. e.g. \(\mathcal{V}^1(3)=\{-1, 0, 1\}\). The generalized convolution in the following equation relaxes the above equation.
where \(\mathcal{N}^D\) is a set of offsets that define the shape of a kernel and \(\mathcal{N}^D(\mathbf{u}, \mathcal{C}^\text{in})= \{\mathbf{i} | \mathbf{u} + \mathbf{i} \in \mathcal{C}^\text{in}, \mathbf{i} \in \mathcal{N}^D \}\) as the set of offsets from the current center, \(\mathbf{u}\), that exist in \(\mathcal{C}^\text{in}\). \(\mathcal{C}^\text{in}\) and \(\mathcal{C}^\text{out}\) are predefined input and output coordinates of sparse tensors. First, note that the input coordinates and output coordinates are not necessarily the same. Second, we define the shape of the convolution kernel arbitrarily with \(\mathcal{N}^D\). This generalization encompasses many special cases such as the dilated convolution and typical hypercubic kernels. Another interesting special case is the sparse submanifold convolution when we set \(\mathcal{C}^\text{out} = \mathcal{C}^\text{in}\) and \(\mathcal{N}^D = \mathcal{V}^D(K)\). If we set \(\mathcal{C}^\text{in} = \mathcal{C}^\text{out} = \mathbb{Z}^D\) and \(\mathcal{N}^D = \mathcal{V}^D(K)\), the generalized convolution on a sparse tensor becomes the conventional dense convolution. If we define the \(\mathcal{C}^\text{in}\) and \(\mathcal{C}^\text{out}\) as multiples of a natural number and \(\mathcal{N}^D = \mathcal{V}^D(K)\), we have a strided dense convolution.
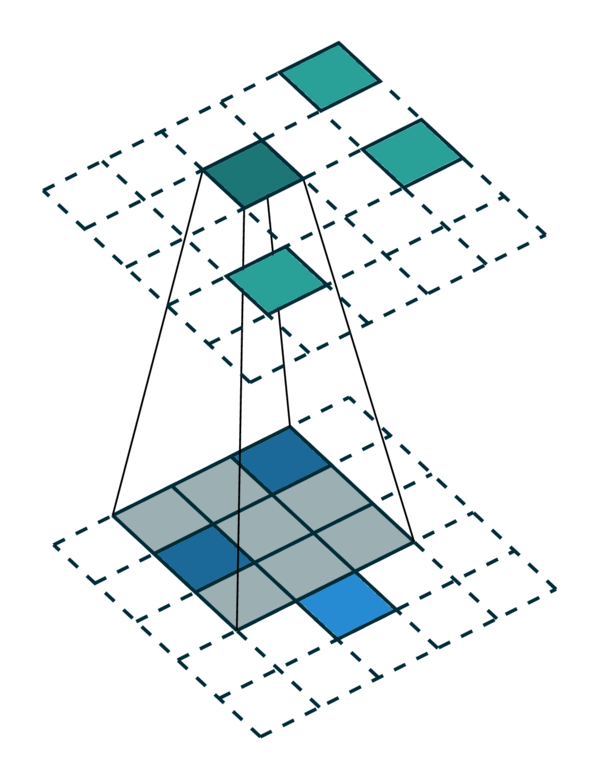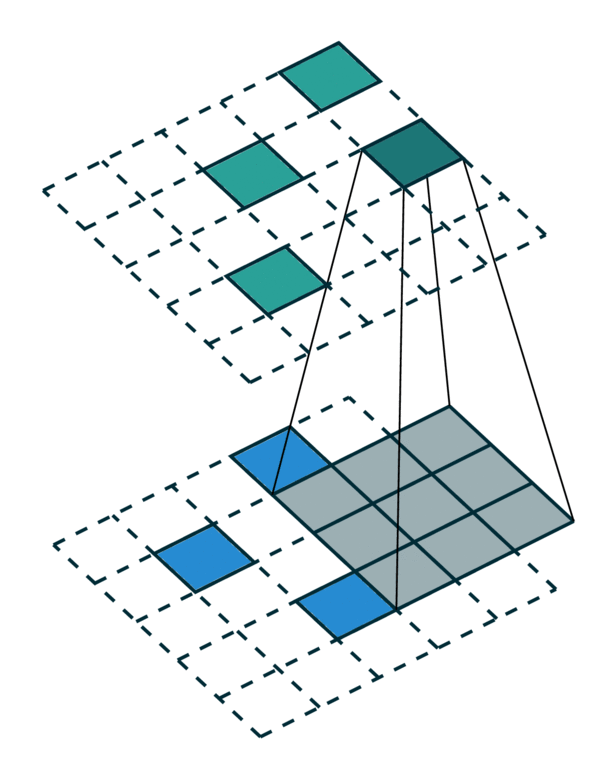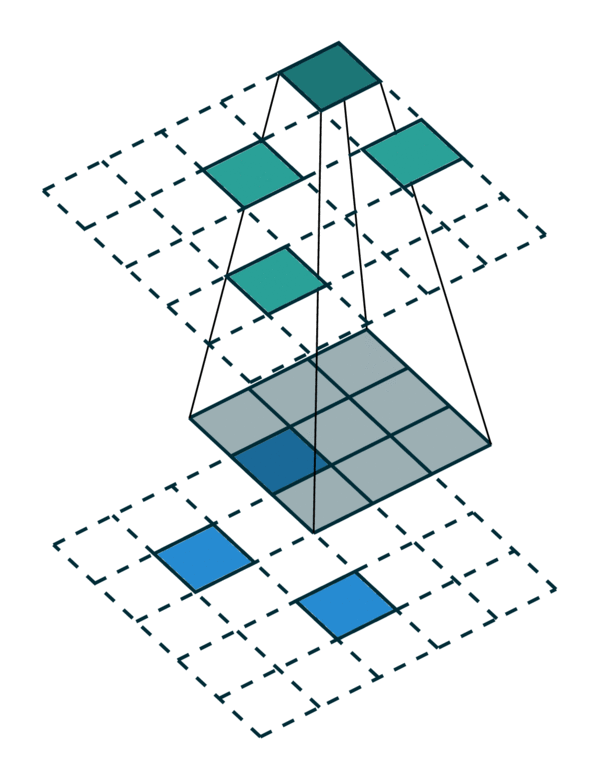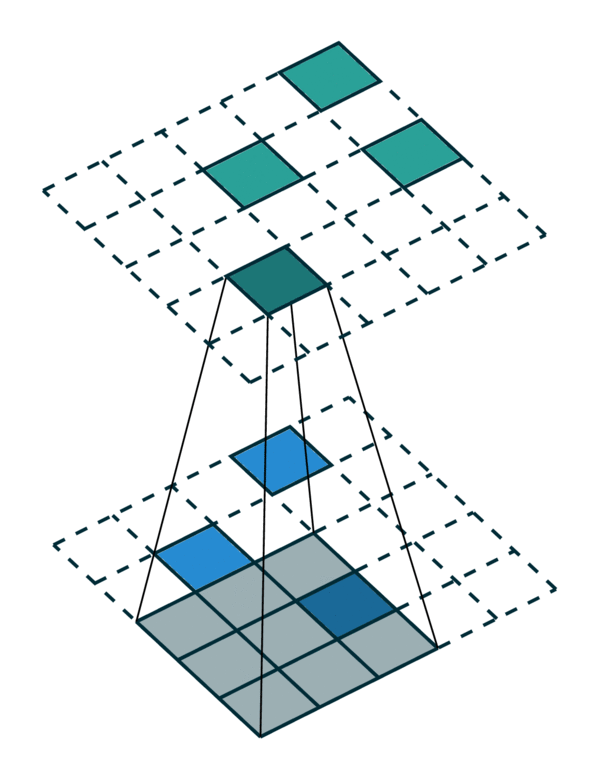
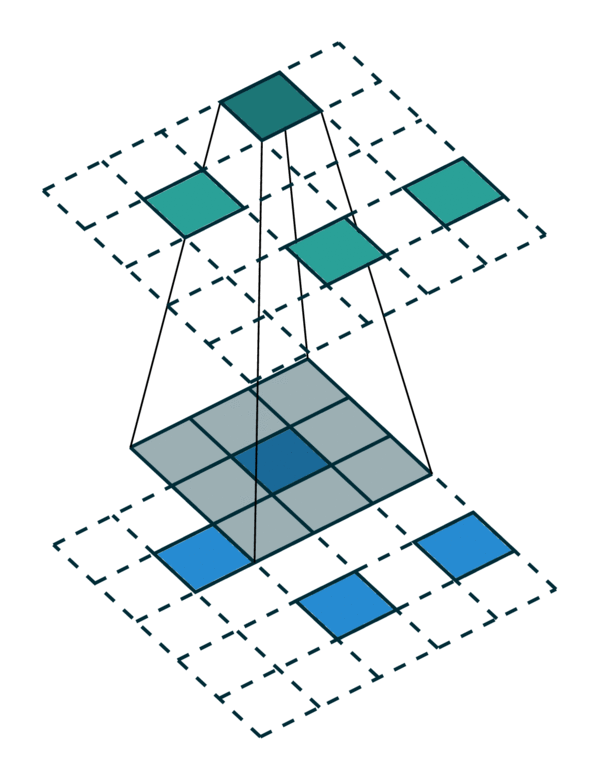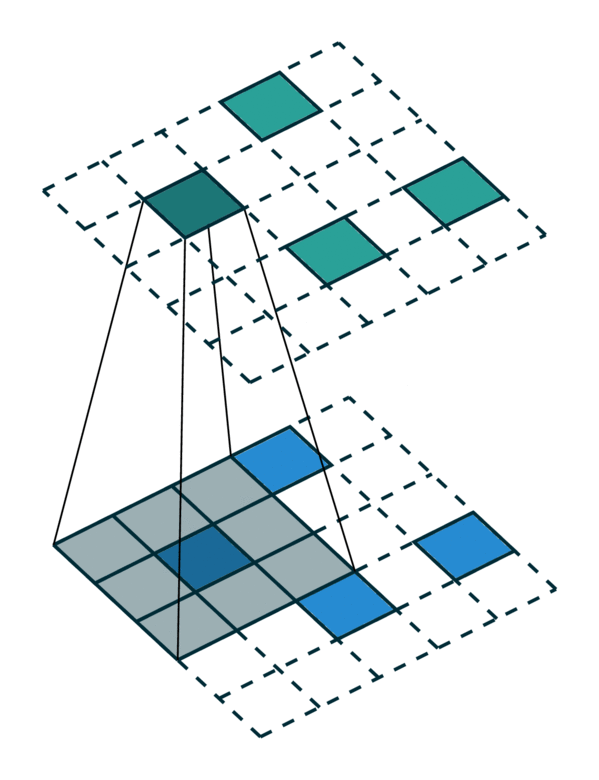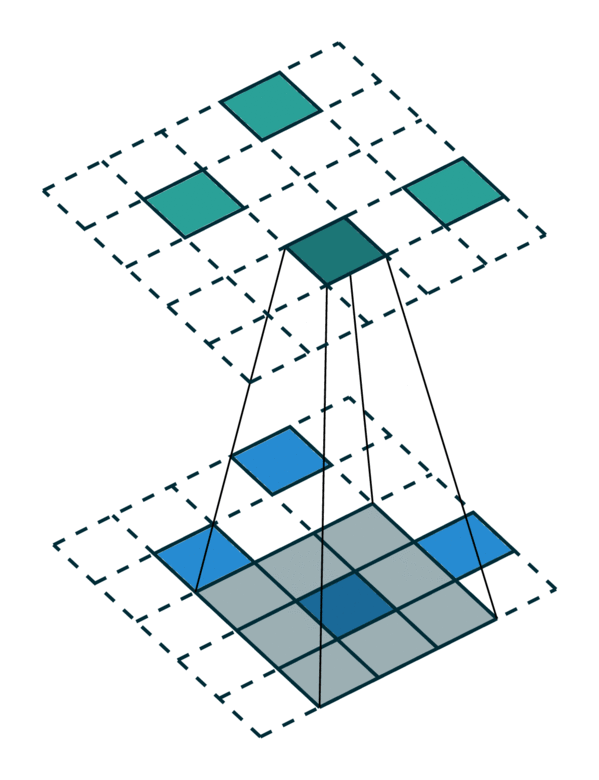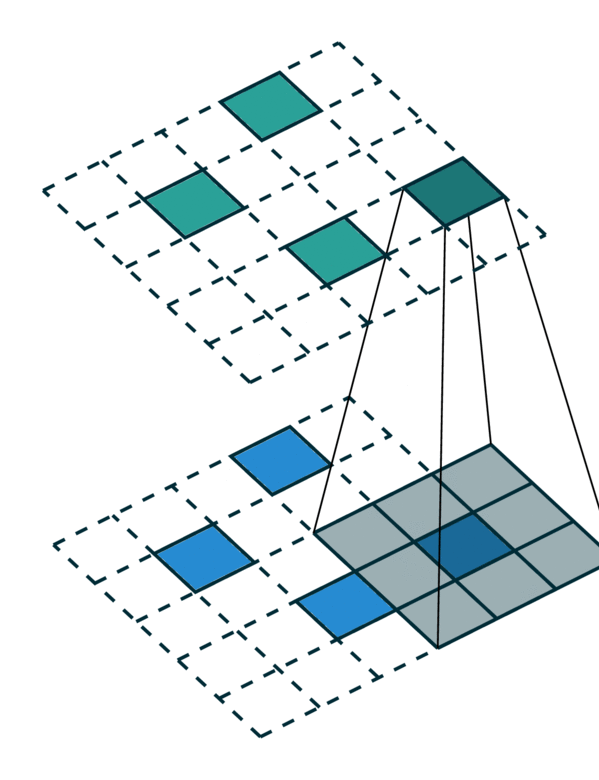
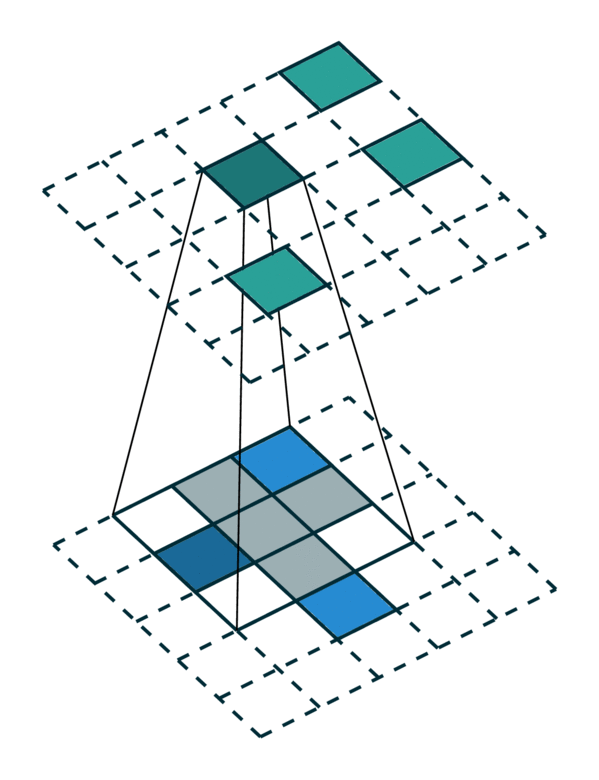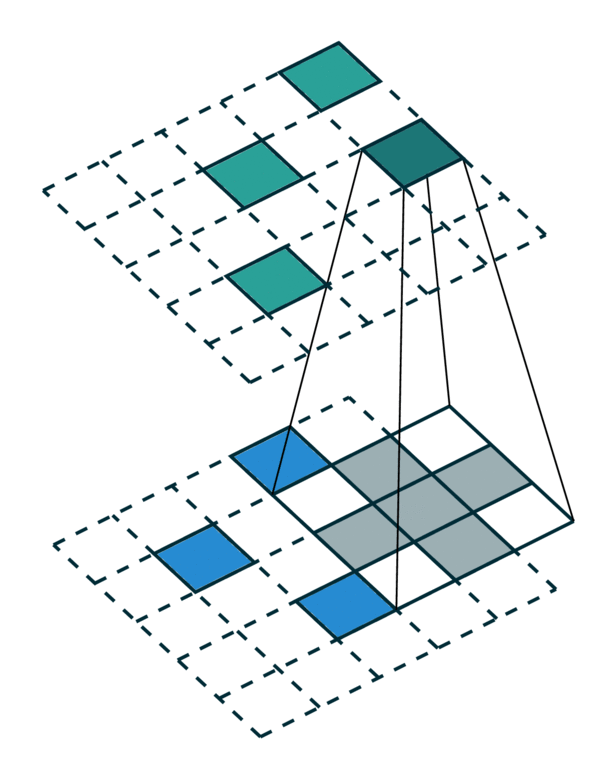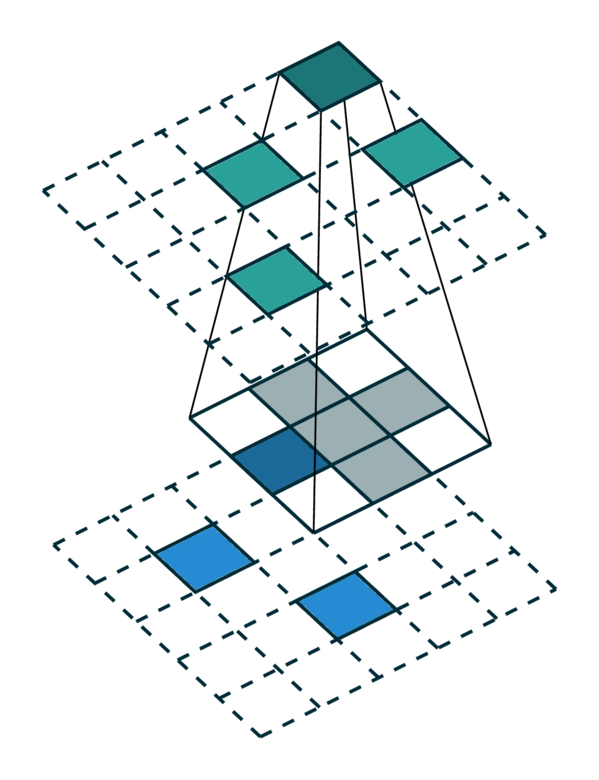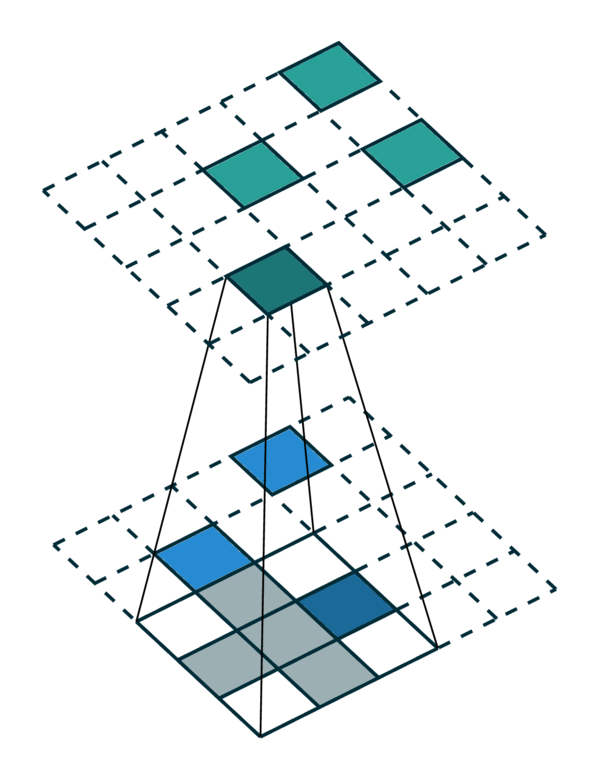
We visualize a simple 2D image convolution on a dense tensor and a sparse tensor. Note that the order of convolution on a sparse tensor is not sequential.
Dense Tensor |
Sparse Tensor |
|---|---|
[Photo Credit: Chris Choy] |
|
To efficiently compute the convolution on a sparse tensor, we must find how each non-zero element in an input sparse tensor is mapped to the output sparse tensor. We call this mapping a kernel map [3] since it defines how an input is mapped to an output through a kernel. Please refer to the terminology page for more details.
Special Cases of Generalized Convolution¶
The generalized convolution encompasses all discrete convolution as its special cases. We will go over a few special cases in this section. First, when the input and output coordinates are all elements on a grid. i.e. a dense tensor, the generalized convolution is equivalent to regular convolution on a dense tensor. Second, when the input and output coordinates are the coordinates of non-zero elements on a sparse tensor, the generalized convolution becomes the sparse convolution [2]. Also, when we use a hyper-cross shaped kernel [3], the generalized convolution is equivalent to the separable convolution.
Same in/out coordinates |
Arbitrary in/out coordinates |
Generalized Convolution |
|---|---|---|
[Photo Credit: Chris Choy] |
||