Definitions and Terminology¶
Sparse Tensor¶
A sparse tensor is a high-dimensional extension of a sparse matrix where non-zero elements are represented as a set of indices \(\mathcal{C}\) and associated values (or features) \(\mathcal{F}\). We use the COOrdinate list (COO) format to save a sparse tensor [1]. This representation is simply a concatenation of coordinates into a matrix \(C\) and associated values or features \(F\). In traditional sparse tensor, indices or coordinates have to be non-negative integers, whereas, in Minkowski Engine, negative coordinates are also valid coordinates. A final sparse tensor \(\mathscr{T}\) with \(D\) dimensional coordinates is a rank-\(D\) tensor if features are scalars, or a rank-\(D + 1\) if features are vectors.
In sum, a sparse tensor consists of a set of coordinates \(\mathcal{C}\) or equivalently a coordinate matrix \(C \in \mathbb{Z}^{N \times D}\) and associated features \(\mathcal{F}\) or a feature matrix \(F \in \mathbb{R}^{N \times N_F}\) where \(N\) is the number of non-zero elements within a sparse tensor, \(D\) is the dimension of the space, and \(N_F\) is the number of channels. The rest of the elements in a sparse tensor is 0.
Tensor Stride¶
A receptive field size of a neuron is defined as the maximum distance along one axis between pixels in the input image that the neuron in a layer can see. For example, if we process an image with two convolution layers with kernel size 3 and stride 2, the receptive field size after the first convolution layer is 3; and the receptive field size after the second convolution layer is 7. This is due to the fact that the second convolution layer sees the feature map that subsamples the image with the factor of 2 or stride 2. Here, the stride refers to the distance between neurons. The feature map after the first convolution has the stride size 2 and that after the second convolution has the stride size 4. Similarly, if we use transposed convolutions (deconv, upconv), we reduce the stride.
We define a tensor stride to be the high-dimensional counterpart of these 2D strides in the above example. When we use pooling or convolution layers with stride greater than 1, the tensor stride of the output feature map increases by the factor of the stride of the layer.
Coordinate Manager¶
Many basic operations such as convolution, pooling, etc, require finding neighbors between non-zero elements. If we use a strided convolution or pooling layer, we need to generate a new set of output coordinates that are different from the input coordinates. All these coordinate-related operations are all managed by a coordinate manager. One thing to note is that coordinate managers cache all coordinates and kernel maps as these coordinates and kernel maps are reused very frequently. For example, in many conventional neural networks, we repeat the same operations in series multiple times such as multiple residual blocks in a ResNet or a DenseNet. Thus, instead of recomputing the same coordinates and same kernel maps, a coordinate manager caches all these and reuses if it detects the same operation in the dictionary.
In Minkowski Engine, we create a coordinate manager when MinkowskiEngine.SparseTensor is initialized. You can optionally share an existing coordinate manager with a new MinkowskiEngine.SparseTensor by providing optional coordinate manager argument during initialization. You can access the coordinate manager of a sparse tensor with MinkowskiEngine.SparseTensor.coords_man.
Coordinate Key¶
Within a coordinate manager, all objects are cached using an unordered map. A coordinate key is a hash key for the unordered map that caches the coordinates of sparse tensors. If two sparse tensors have the same coordinate manager and the same coordinate key, then the coordinates of the sparse tensors are identical and they share the same memory space.
Kernel Map¶
A sparse tensor consists of a set of coordinates \(C \in \mathbb{Z}^{N \times D}\) and associated features \(F \in \mathbb{R}^{N \times N_F}\) where \(N\) is the number of non-zero elements within a sparse tensor, \(D\) is the dimension of the space, and \(N_F\) is the number of channels. To find how a sparse tensor is mapped to another sparse tensor using a spatially local operations such as convolution or pooling, we need to find which coordinate in the input sparse tensor is mapped to which coordinate in the output sparse tensor.
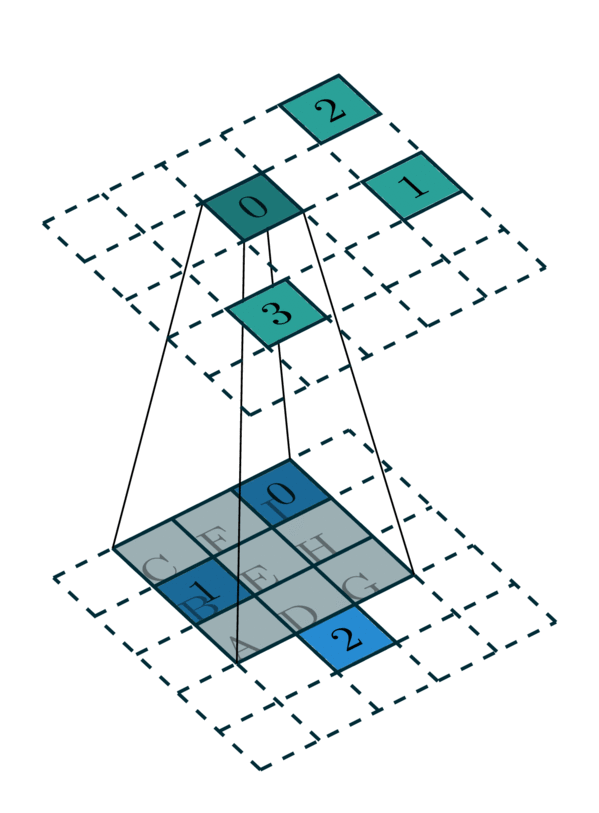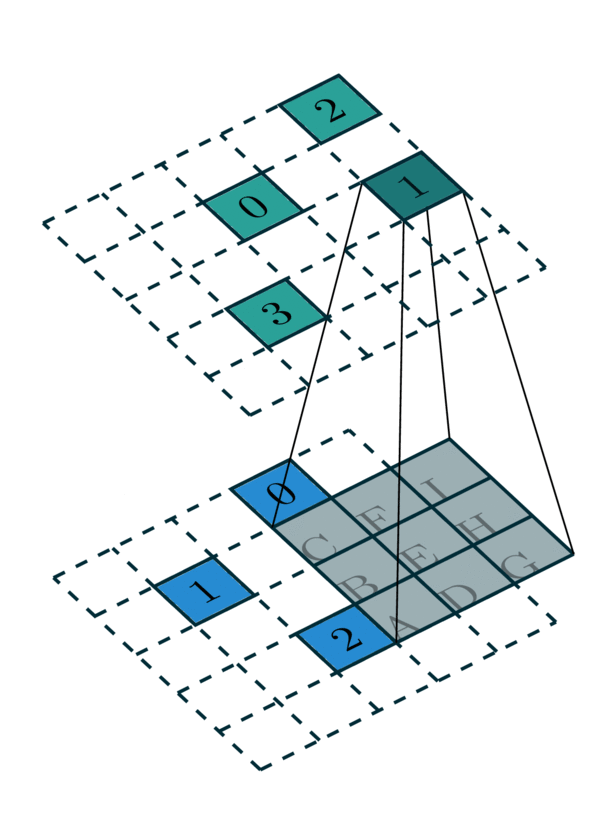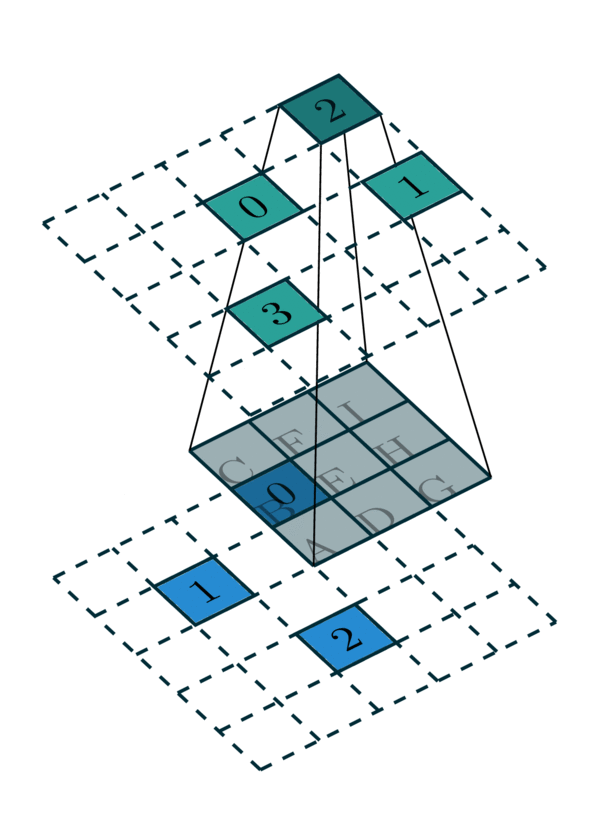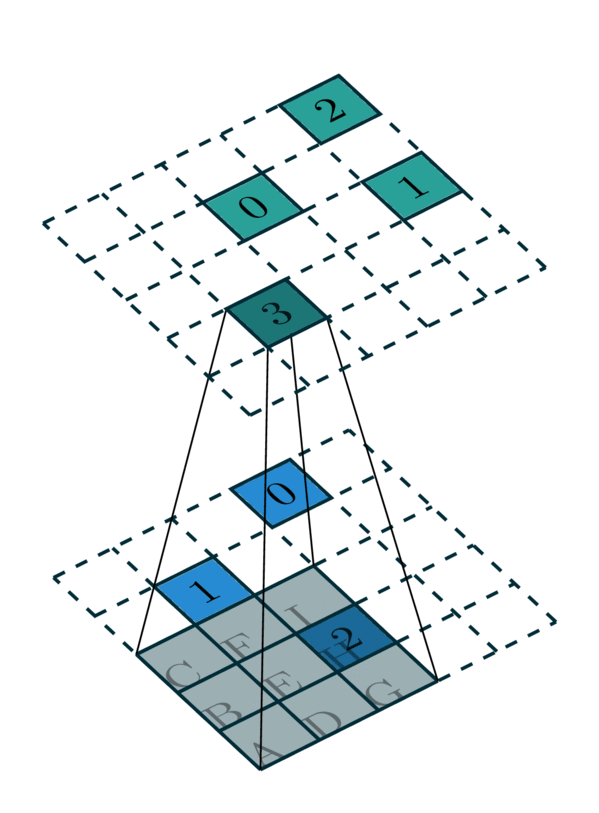
We call this mapping from an input sparse tensor to an output sparse tensor a kernel map. For example, a 2D convolution with kernel size 3 has a \(3 \times 3\) convolution kernel, which consists of 9 weight matrices. Some input coordinates are mapped to corresponding output coordinates with each kernel. We represent a map as a pair of lists of integers: the in map \(\mathbf{I}\) and the out map \(\mathbf{O}\). An integer in an in map \(i \in \mathbf{I}\) indicates the row index of the coordinate matrix or the feature matrix of an input sparse tensor. Similarly, an integer in the out map \(o \in \mathbf{O}\) also indicates the row index of the coordinate matrix of an output sparse tensor. The integers in the lists are ordered in a way that k-th element \(i_k\) in the in map corresponds to the k-th element \(o_k\) of the out map. In sum, \((\mathbf{I} \rightarrow \mathbf{O})\) defines how the row indices of input feature \(F_I\) maps to the row indices of output feature \(F_O\).
Since a single kernel map defines a map for one specific cell of a convolution kernel, a convolution requires multiple kernel maps. In the case of a \(3 \times 3\) convolution in this example, we need 9 maps to define a complete kernel map.
Convolution Kernel Map |
[Photo Credit: Chris Choy] |
In this example, we require 9 kernel maps for all \(3\times 3\) kernel. However, some of these kernel maps do not have elements. As the convolution kernel goes over all the coordinates, we extract kernel maps:
Kernel B: 1 → 0
Kernel B: 0 → 2
Kernel H: 2 → 3
Kernel I: 0 → 0