Interoperability#
Warp can interoperate with other Python-based frameworks such as NumPy through standard interface protocols.
Warp supports passing external arrays to kernels directly, as long as they implement the __array__, __array_interface__, or __cuda_array_interface__ protocols. This works with many common frameworks like NumPy, CuPy, or PyTorch.
For example, we can use NumPy arrays directly when launching Warp kernels on the CPU:
import numpy as np
import warp as wp
@wp.kernel
def saxpy(x: wp.array(dtype=float), y: wp.array(dtype=float), a: float):
i = wp.tid()
y[i] = a * x[i] + y[i]
x = np.arange(n, dtype=np.float32)
y = np.ones(n, dtype=np.float32)
wp.launch(saxpy, dim=n, inputs=[x, y, 1.0], device="cpu")
Likewise, we can use CuPy arrays on a CUDA device:
import cupy as cp
with cp.cuda.Device(0):
x = cp.arange(n, dtype=cp.float32)
y = cp.ones(n, dtype=cp.float32)
wp.launch(saxpy, dim=n, inputs=[x, y, 1.0], device="cuda:0")
Note that with CUDA arrays, it’s important to ensure that the device on which the arrays reside is the same as the device on which the kernel is launched.
PyTorch supports both CPU and GPU tensors and both kinds can be passed to Warp kernels on the appropriate device.
import random
import torch
if random.choice([False, True]):
device = "cpu"
else:
device = "cuda:0"
x = torch.arange(n, dtype=torch.float32, device=device)
y = torch.ones(n, dtype=torch.float32, device=device)
wp.launch(saxpy, dim=n, inputs=[x, y, 1.0], device=device)
NumPy#
Warp arrays may be converted to a NumPy array through the array.numpy() method. When the Warp array lives on
the cpu device this will return a zero-copy view onto the underlying Warp allocation. If the array lives on a
cuda device then it will first be copied back to a temporary buffer and copied to NumPy.
Warp CPU arrays also implement the __array_interface__ protocol and so can be used to construct NumPy arrays
directly:
w = wp.array([1.0, 2.0, 3.0], dtype=float, device="cpu")
a = np.array(w)
print(a)
> [1. 2. 3.]
Data type conversion utilities are also available for convenience:
warp_type = wp.float32
...
numpy_type = wp.dtype_to_numpy(warp_type)
...
a = wp.zeros(n, dtype=warp_type)
b = np.zeros(n, dtype=numpy_type)
To create Warp arrays from NumPy arrays, use warp.from_numpy()
or pass the NumPy array as the data argument of the warp.array constructor directly.
- warp.from_numpy(
- arr,
- dtype=None,
- shape=None,
- device=None,
- requires_grad=False,
Returns a Warp array created from a NumPy array.
- Parameters:
arr (ndarray) – The NumPy array providing the data to construct the Warp array.
dtype (type | None) – The data type of the new Warp array. If this is not provided, the data type will be inferred.
device (Device | str | None) – The device on which the Warp array will be constructed.
requires_grad (bool) – Whether gradients will be tracked for this array.
- Raises:
RuntimeError – The data type of the NumPy array is not supported.
- Return type:
PyTorch#
Warp provides helper functions to convert arrays to/from PyTorch:
w = wp.array([1.0, 2.0, 3.0], dtype=float, device="cpu")
# convert to Torch tensor
t = wp.to_torch(w)
# convert from Torch tensor
w = wp.from_torch(t)
These helper functions allow the conversion of Warp arrays to/from PyTorch tensors without copying the underlying data. At the same time, if available, gradient arrays and tensors are converted to/from PyTorch autograd tensors, allowing the use of Warp arrays in PyTorch autograd computations.
- warp.from_torch(
- t,
- dtype=None,
- requires_grad=None,
- grad=None,
- return_ctype=False,
Convert a Torch tensor to a Warp array without copying the data.
- Parameters:
t (torch.Tensor) – The torch tensor to wrap.
dtype (warp.dtype, optional) – The target data type of the resulting Warp array. Defaults to the tensor value type mapped to a Warp array value type.
requires_grad (bool, optional) – Whether the resulting array should wrap the tensor’s gradient, if it exists (the grad tensor will be allocated otherwise). Defaults to the tensor’s requires_grad value.
return_ctype (bool, optional) – Whether to return a low-level array descriptor instead of a
wp.arrayobject (faster). The descriptor can be passed to Warp kernels.
- Returns:
The wrapped array or array descriptor.
- Return type:
- warp.to_torch(a, requires_grad=None)[source]#
Convert a Warp array to a Torch tensor without copying the data.
- Parameters:
a (warp.array) – The Warp array to convert.
requires_grad (bool, optional) – Whether the resulting tensor should convert the array’s gradient, if it exists, to a grad tensor. Defaults to the array’s requires_grad value.
- Returns:
The converted tensor.
- Return type:
- warp.device_from_torch(torch_device)[source]#
Return the Warp device corresponding to a Torch device.
- Parameters:
torch_device (torch.device or str) – Torch device identifier
- Raises:
RuntimeError – Torch device does not have a corresponding Warp device
- Return type:
- warp.device_to_torch(warp_device)[source]#
Return the Torch device string corresponding to a Warp device.
- Parameters:
warp_device (Device | str | None) – An identifier that can be resolved to a
warp._src.context.Device.- Raises:
RuntimeError – The Warp device is not compatible with PyTorch.
- Return type:
- warp.dtype_from_torch(torch_dtype)[source]#
Return the Warp dtype corresponding to a Torch dtype.
- Parameters:
torch_dtype – A
torch.dtypethat has a corresponding Warp data type. Currentlytorch.bfloat16,torch.complex64, andtorch.complex128are not supported.- Raises:
TypeError – Unable to find a corresponding Warp data type.
- warp.dtype_to_torch(warp_dtype)[source]#
Return the Torch dtype corresponding to a Warp dtype.
- Parameters:
warp_dtype – A Warp data type that has a corresponding
torch.dtype.warp.uint16,warp.uint32, andwarp.uint64are mapped to the signed integertorch.dtypeof the same width.- Raises:
TypeError – Unable to find a corresponding PyTorch data type.
To convert a PyTorch CUDA stream to a Warp CUDA stream and vice versa, Warp provides the following functions:
- warp.stream_from_torch(stream_or_device=None)[source]#
Convert from a Torch CUDA stream to a Warp CUDA stream.
- warp.stream_to_torch(stream_or_device=None)[source]#
Convert from a Warp CUDA stream to a Torch CUDA stream.
Example: Optimization using warp.from_torch()#
An example usage of minimizing a loss function over an array of 2D points written in Warp via PyTorch’s Adam optimizer
using warp.from_torch() is as follows:
import warp as wp
import torch
@wp.kernel()
def loss(xs: wp.array(dtype=float, ndim=2), l: wp.array(dtype=float)):
tid = wp.tid()
wp.atomic_add(l, 0, xs[tid, 0] ** 2.0 + xs[tid, 1] ** 2.0)
# indicate requires_grad so that Warp can accumulate gradients in the grad buffers
xs = torch.randn(100, 2, requires_grad=True)
l = torch.zeros(1, requires_grad=True)
opt = torch.optim.Adam([xs], lr=0.1)
wp_xs = wp.from_torch(xs)
wp_l = wp.from_torch(l)
tape = wp.Tape()
with tape:
# record the loss function kernel launch on the tape
wp.launch(loss, dim=len(xs), inputs=[wp_xs], outputs=[wp_l], device=wp_xs.device)
for i in range(500):
tape.zero()
tape.backward(loss=wp_l) # compute gradients
# now xs.grad will be populated with the gradients computed by Warp
opt.step() # update xs (and thereby wp_xs)
# these lines are only needed for evaluating the loss
# (the optimization just needs the gradient, not the loss value)
wp_l.zero_()
wp.launch(loss, dim=len(xs), inputs=[wp_xs], outputs=[wp_l], device=wp_xs.device)
print(f"{i}\tloss: {l.item()}")
Example: Optimization using warp.to_torch#
Less code is needed when we declare the optimization variables directly in Warp and use warp.to_torch() to convert them to PyTorch tensors.
Here, we revisit the same example from above where now only a single conversion to a PyTorch tensor is needed to supply Adam with the optimization variables:
import warp as wp
import numpy as np
import torch
@wp.kernel()
def loss(xs: wp.array(dtype=float, ndim=2), l: wp.array(dtype=float)):
tid = wp.tid()
wp.atomic_add(l, 0, xs[tid, 0] ** 2.0 + xs[tid, 1] ** 2.0)
# initialize the optimization variables in Warp
xs = wp.array(np.random.randn(100, 2), dtype=wp.float32, requires_grad=True)
l = wp.zeros(1, dtype=wp.float32, requires_grad=True)
# just a single wp.to_torch call is needed, Adam optimizes using the Warp array gradients
opt = torch.optim.Adam([wp.to_torch(xs)], lr=0.1)
tape = wp.Tape()
with tape:
wp.launch(loss, dim=len(xs), inputs=[xs], outputs=[l], device=xs.device)
for i in range(500):
tape.zero()
tape.backward(loss=l)
opt.step()
l.zero_()
wp.launch(loss, dim=len(xs), inputs=[xs], outputs=[l], device=xs.device)
print(f"{i}\tloss: {l.numpy()[0]}")
Example: Optimization using torch.autograd.function (PyTorch <= 2.3.1)#
One can insert Warp kernel launches in a PyTorch graph by defining a torch.autograd.Function class, which
requires forward and backward functions to be defined. After mapping incoming PyTorch tensors to Warp arrays, a Warp kernel
may be launched in the usual way. In the backward pass, the same kernel’s adjoint may be launched by
setting adjoint = True in wp.launch(). Alternatively, the user may choose to rely on Warp’s tape.
In the following example, we demonstrate how Warp may be used to evaluate the Rosenbrock function in an optimization context.
import warp as wp
import numpy as np
import torch
# Define the Rosenbrock function
@wp.func
def rosenbrock(x: float, y: float):
return (1.0 - x) ** 2.0 + 100.0 * (y - x**2.0) ** 2.0
@wp.kernel
def eval_rosenbrock(
xs: wp.array(dtype=wp.vec2),
# outputs
z: wp.array(dtype=float),
):
i = wp.tid()
x = xs[i]
z[i] = rosenbrock(x[0], x[1])
class Rosenbrock(torch.autograd.Function):
@staticmethod
def forward(ctx, xy, num_points):
ctx.xy = wp.from_torch(xy, dtype=wp.vec2, requires_grad=True)
ctx.num_points = num_points
# allocate output
ctx.z = wp.zeros(num_points, requires_grad=True)
wp.launch(
kernel=eval_rosenbrock,
dim=ctx.num_points,
inputs=[ctx.xy],
outputs=[ctx.z]
)
return wp.to_torch(ctx.z)
@staticmethod
def backward(ctx, adj_z):
# map incoming Torch grads to our output variables
ctx.z.grad = wp.from_torch(adj_z)
wp.launch(
kernel=eval_rosenbrock,
dim=ctx.num_points,
inputs=[ctx.xy],
outputs=[ctx.z],
adj_inputs=[ctx.xy.grad],
adj_outputs=[ctx.z.grad],
adjoint=True
)
# return adjoint w.r.t. inputs
return (wp.to_torch(ctx.xy.grad), None)
num_points = 1500
learning_rate = 5e-2
torch_device = wp.device_to_torch(wp.get_device())
rng = np.random.default_rng(42)
xy = torch.tensor(rng.normal(size=(num_points, 2)), dtype=torch.float32, requires_grad=True, device=torch_device)
opt = torch.optim.Adam([xy], lr=learning_rate)
for _ in range(10000):
# step
opt.zero_grad()
z = Rosenbrock.apply(xy, num_points)
z.backward(torch.ones_like(z))
opt.step()
# minimum at (1, 1)
xy_np = xy.numpy(force=True)
print(np.mean(xy_np, axis=0))
Note that if Warp code is wrapped in a torch.autograd.Function that gets called in torch.compile(), it will automatically
exclude that function from compiler optimizations. If your script uses torch.compile(),
we recommend using PyTorch version 2.3.0+, which has improvements that address this scenario.
Example: Optimization using PyTorch custom operators (PyTorch >= 2.4.0)#
PyTorch 2.4+ introduced custom operators to replace
PyTorch autograd functions. These treat arbitrary Python functions (including Warp calls) as opaque callables, which prevents
torch.compile() from tracing into them. This means that forward PyTorch graph evaluations that include Warp kernel launches can be safely accelerated with
torch.compile(). We can re-write the previous example using custom operators as follows:
import warp as wp
import numpy as np
import torch
# Define the Rosenbrock function
@wp.func
def rosenbrock(x: float, y: float):
return (1.0 - x) ** 2.0 + 100.0 * (y - x**2.0) ** 2.0
@wp.kernel
def eval_rosenbrock(
xy: wp.array(dtype=wp.vec2),
# outputs
z: wp.array(dtype=float),
):
i = wp.tid()
v = xy[i]
z[i] = rosenbrock(v[0], v[1])
@torch.library.custom_op("wp::warp_rosenbrock", mutates_args=())
def warp_rosenbrock(xy: torch.Tensor, num_points: int) -> torch.Tensor:
wp_xy = wp.from_torch(xy, dtype=wp.vec2)
wp_z = wp.zeros(num_points, dtype=wp.float32)
wp.launch(kernel=eval_rosenbrock, dim=num_points, inputs=[wp_xy], outputs=[wp_z])
return wp.to_torch(wp_z)
@warp_rosenbrock.register_fake
def _(xy, num_points):
return torch.empty(num_points, dtype=torch.float32)
@torch.library.custom_op("wp::warp_rosenbrock_backward", mutates_args=())
def warp_rosenbrock_backward(
xy: torch.Tensor, num_points: int, z: torch.Tensor, adj_z: torch.Tensor
) -> torch.Tensor:
wp_xy = wp.from_torch(xy, dtype=wp.vec2)
wp_z = wp.from_torch(z, requires_grad=False)
wp_adj_z = wp.from_torch(adj_z, requires_grad=False)
wp.launch(
kernel=eval_rosenbrock,
dim=num_points,
inputs=[wp_xy],
outputs=[wp_z],
adj_inputs=[wp_xy.grad],
adj_outputs=[wp_adj_z],
adjoint=True,
)
return wp.to_torch(wp_xy.grad)
@warp_rosenbrock_backward.register_fake
def _(xy, num_points, z, adj_z):
return torch.empty_like(xy)
def backward(ctx, adj_z):
ctx.xy.grad = warp_rosenbrock_backward(ctx.xy, ctx.num_points, ctx.z, adj_z)
return ctx.xy.grad, None
def setup_context(ctx, inputs, output):
ctx.xy, ctx.num_points = inputs
ctx.z = output
warp_rosenbrock.register_autograd(backward, setup_context=setup_context)
num_points = 1500
learning_rate = 5e-2
torch_device = wp.device_to_torch(wp.get_device())
rng = np.random.default_rng(42)
xy = torch.tensor(rng.normal(size=(num_points, 2)), dtype=torch.float32, requires_grad=True, device=torch_device)
opt = torch.optim.Adam([xy], lr=learning_rate)
@torch.compile(fullgraph=True)
def forward():
global xy, num_points
z = warp_rosenbrock(xy, num_points)
return z
for _ in range(10000):
# step
opt.zero_grad()
z = forward()
z.backward(torch.ones_like(z))
opt.step()
# minimum at (1, 1)
xy_np = xy.numpy(force=True)
print(np.mean(xy_np, axis=0))
Performance Notes#
The wp.from_torch() function creates a Warp array object that shares data with a PyTorch tensor.
Although this function does not copy the data, there is always some CPU overhead during the conversion.
If these conversions happen frequently, the overall program performance may suffer.
As a general rule, repeated conversions of the same tensor should be avoided. Instead of:
x_t = torch.arange(n, dtype=torch.float32, device=device)
y_t = torch.ones(n, dtype=torch.float32, device=device)
for i in range(10):
x_w = wp.from_torch(x_t)
y_w = wp.from_torch(y_t)
wp.launch(saxpy, dim=n, inputs=[x_w, y_w, 1.0], device=device)
Try converting the arrays only once and reuse them:
x_t = torch.arange(n, dtype=torch.float32, device=device)
y_t = torch.ones(n, dtype=torch.float32, device=device)
x_w = wp.from_torch(x_t)
y_w = wp.from_torch(y_t)
for i in range(10):
wp.launch(saxpy, dim=n, inputs=[x_w, y_w, 1.0], device=device)
If reusing arrays is not possible (e.g., a new PyTorch tensor is constructed on every iteration), passing return_ctype=True
to wp.from_torch() should yield better performance.
Setting this argument to True avoids constructing a wp.array object and instead returns a low-level array descriptor.
This descriptor is a simple C structure that can be passed to Warp kernels instead of a wp.array,
but cannot be used in other places that require a wp.array.
for n in range(1, 10):
# get Torch tensors for this iteration
x_t = torch.arange(n, dtype=torch.float32, device=device)
y_t = torch.ones(n, dtype=torch.float32, device=device)
# get Warp array descriptors
x_ctype = wp.from_torch(x_t, return_ctype=True)
y_ctype = wp.from_torch(y_t, return_ctype=True)
wp.launch(saxpy, dim=n, inputs=[x_ctype, y_ctype, 1.0], device=device)
An alternative approach is to pass the PyTorch tensors to Warp kernels directly.
This avoids constructing temporary Warp arrays by leveraging standard array interfaces (like __cuda_array_interface__) supported by both PyTorch and Warp.
The main advantage of this approach is convenience, since there is no need to call any conversion functions.
The main limitation is that it does not handle gradients, because gradient information is not included in the standard array interfaces.
This technique is therefore most suitable for algorithms that do not involve differentiation.
x = torch.arange(n, dtype=torch.float32, device=device)
y = torch.ones(n, dtype=torch.float32, device=device)
for i in range(10):
wp.launch(saxpy, dim=n, inputs=[x, y, 1.0], device=device)
python -m warp.examples.benchmarks.benchmark_interop_torch
Sample output:
5095 ms from_torch(...)
2113 ms from_torch(..., return_ctype=True)
2950 ms direct from torch
The default wp.from_torch() conversion is the slowest.
Passing return_ctype=True is the fastest, because it skips creating temporary Warp array objects.
Passing PyTorch tensors to Warp kernels directly falls somewhere in between.
It skips creating temporary Warp arrays, but accessing the __cuda_array_interface__ attributes of PyTorch tensors
adds overhead because they are initialized on-demand.
Case Study: PyTorch Deferred Gradient Allocation and Warp Interoperability#
When writing custom PyTorch autograd functions that use Warp kernels, whether using analytic gradient kernels or the Warp tape, PyTorch’s deferred gradient allocation can cause unexpected synchronization delays. This case study demonstrates the problem and provides practical solutions.
The Problem: Deferred Gradient Allocation#
PyTorch employs a deferred allocation strategy for gradient tensors. When you create a tensor with requires_grad=True,
PyTorch does not immediately allocate memory for the gradient. Instead, gradients are allocated on-demand during
the backward pass.
However, when wp.from_torch() encounters a tensor with requires_grad=True but no allocated gradient,
it forces the gradient to be allocated immediately. This creates overhead that can significantly impact performance.
When PyTorch later discovers that an external framework has allocated its gradient tensors, it must perform an expensive device-wide synchronization to ensure correctness. This synchronization overhead can significantly impact performance.
Here’s an example that demonstrates the problem:
import warp as wp
import torch
device = 'cuda'
N = 300_000_000
wp.init()
@wp.kernel(enable_backward=False)
def forward_kernel(
a: wp.array(dtype=float),
b: wp.array(dtype=float),
output: wp.array(dtype=float)
):
i = wp.tid()
x = a[i]
y = b[i]
output[i] = x*x + y*y
@wp.kernel(enable_backward=False)
def backward_kernel(
grad_output: wp.array(dtype=float),
a: wp.array(dtype=float),
b: wp.array(dtype=float),
grad_a: wp.array(dtype=float),
grad_b: wp.array(dtype=float)
):
i = wp.tid()
x = a[i]
y = b[i]
adj_z = grad_output[i]
grad_a[i] = 2.0 * x * adj_z
grad_b[i] = 2.0 * y * adj_z
class WarpFunction(torch.autograd.Function):
@staticmethod
def forward(ctx, a, b):
ctx.save_for_backward(a, b)
device = wp.device_from_torch(a.device)
output = torch.empty(N, device=a.device)
wp.launch(
kernel=forward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(a), # ⚠️ Triggers gradient allocation
wp.from_torch(b), # ⚠️ Triggers gradient allocation
wp.from_torch(output),
],
)
return output
@staticmethod
def backward(ctx, grad_output):
a, b = ctx.saved_tensors
device = wp.device_from_torch(a.device)
grad_a = torch.empty_like(a)
grad_b = torch.empty_like(b)
wp.launch(
kernel=backward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(grad_output.contiguous()),
wp.from_torch(a),
wp.from_torch(b),
wp.from_torch(grad_a),
wp.from_torch(grad_b),
],
)
return grad_a, grad_b
a = torch.randn(N, device=device, dtype=torch.float32, requires_grad=True)
b = torch.randn(N, device=device, dtype=torch.float32, requires_grad=True)
torch.cuda.synchronize()
for i in range(TRIALS):
with wp.ScopedTimer(f"TRIAL {i}", use_nvtx=True, synchronize=True):
with wp.ScopedTimer("Create Tensors", use_nvtx=True, synchronize=True):
a_torch = a.clone().detach().requires_grad_(True)
b_torch = b.clone().detach().requires_grad_(True)
with wp.ScopedTimer("Forward", use_nvtx=True, synchronize=True):
output_warp = WarpFunction.apply(a_torch, b_torch)
with wp.ScopedTimer("Loss", use_nvtx=True, synchronize=True):
loss_warp = output_warp.sum()
with wp.ScopedTimer("Backward", use_nvtx=True, synchronize=True):
loss_warp.backward()
When profiling this code with NVIDIA Nsight Systems, significant gaps appear in the GPU timeline, indicating device-wide synchronization events:
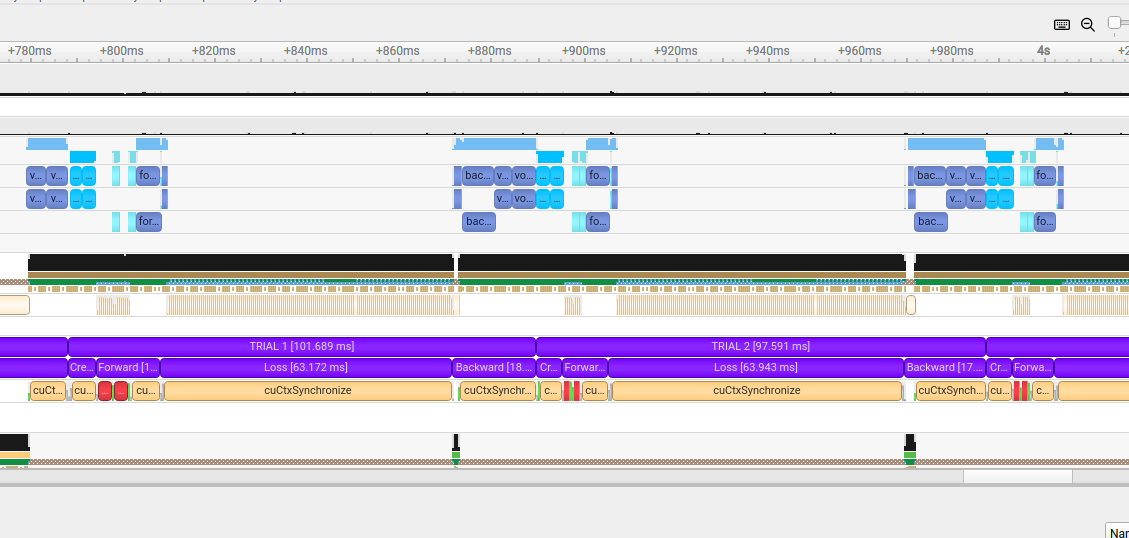
NVIDIA Nsight Systems timeline showing synchronization gaps between Warp kernel launches and PyTorch operations.#
The gaps represent device-wide synchronizations triggered when PyTorch discovers externally allocated gradients.
This problem is particularly severe in this benchmark because new tensors (a_torch and b_torch) are created
on each iteration via .clone().detach().requires_grad_(True). Since these fresh tensors have requires_grad=True
but no pre-allocated gradients, the synchronization penalty is incurred on every single iteration.
Solutions#
There are three approaches to avoid this synchronization overhead, depending on your use case:
Solution A: Disable Gradient Tracking in wp.from_torch()
The simplest solution is to pass requires_grad=False to wp.from_torch(), preventing Warp from
auto-allocating gradients:
@staticmethod
def forward(ctx, a, b):
ctx.save_for_backward(a, b)
device = wp.device_from_torch(a.device)
output = torch.empty(N, device=a.device)
wp.launch(
kernel=forward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(a, requires_grad=False), # ✓ No gradient allocation
wp.from_torch(b, requires_grad=False), # ✓ No gradient allocation
wp.from_torch(output, requires_grad=False),
],
)
return output
@staticmethod
def backward(ctx, grad_output):
a, b = ctx.saved_tensors
device = wp.device_from_torch(a.device)
grad_a = torch.empty_like(a)
grad_b = torch.empty_like(b)
wp.launch(
kernel=backward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(grad_output.contiguous(), requires_grad=False),
wp.from_torch(a, requires_grad=False),
wp.from_torch(b, requires_grad=False),
wp.from_torch(grad_a, requires_grad=False),
wp.from_torch(grad_b, requires_grad=False),
],
)
return grad_a, grad_b
This approach works well when you’re managing forward and gradient tensors separately and don’t need Warp to track gradients automatically.
Solution B: Detach Tensors from the PyTorch Graph
When managing gradients outside PyTorch’s autograd graph, detaching tensors is a clean approach:
@staticmethod
def forward(ctx, a, b):
# Store detached tensors - we'll manage gradients manually
ctx.a = a.detach()
ctx.b = b.detach()
device = wp.device_from_torch(a.device)
output = torch.empty(N, device=a.device)
wp.launch(
kernel=forward_kernel,
dim=(N),
device=device,
inputs=[
ctx.a, # ✓ Detached, no requires_grad
ctx.b, # ✓ Detached, no requires_grad
output,
],
)
return output
@staticmethod
def backward(ctx, grad_output):
device = wp.device_from_torch(ctx.a.device)
grad_a = torch.empty_like(ctx.a)
grad_b = torch.empty_like(ctx.b)
wp.launch(
kernel=backward_kernel,
dim=(N),
device=device,
inputs=[
grad_output.detach(),
ctx.a, # ✓ Already detached
ctx.b, # ✓ Already detached
grad_a,
grad_b,
],
)
return grad_a, grad_b
Detaching removes tensors from PyTorch’s computational graph (and clears requires_grad), making it clear
that gradient management happens outside PyTorch’s autograd system.
Solution C: Pre-allocate Gradients with PyTorch
Alternatively, you can pre-allocate gradients using PyTorch’s allocator before passing tensors to Warp. This approach works for both analytic gradient kernels and when using the Warp tape.
Variant 1: With Analytic Gradient Kernels
@staticmethod
def forward(ctx, a, b):
# Pre-allocate gradients using PyTorch's allocator
if a.grad is None:
a.grad = torch.empty_like(a)
if b.grad is None:
b.grad = torch.empty_like(b)
ctx.save_for_backward(a, b)
device = wp.device_from_torch(a.device)
output = torch.empty(N, device=a.device)
wp.launch(
kernel=forward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(a),
wp.from_torch(b),
wp.from_torch(output),
],
)
return output
@staticmethod
def backward(ctx, grad_output):
a, b = ctx.saved_tensors
device = wp.device_from_torch(a.device)
# Now we can use a.grad and b.grad directly
wp.launch(
kernel=backward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(grad_output.contiguous()),
wp.from_torch(a),
wp.from_torch(b),
wp.from_torch(a.grad), # ✓ Allocated by PyTorch
wp.from_torch(b.grad), # ✓ Allocated by PyTorch
],
)
return a.grad, b.grad
Variant 2: With Warp’s Tape (Automatic Differentiation)
@staticmethod
def forward(ctx, a, b):
device = wp.device_from_torch(a.device)
output = torch.zeros(N, device=a.device)
# Pre-allocate gradients using PyTorch's allocator
if a.grad is None:
a.grad = torch.empty_like(a)
if b.grad is None:
b.grad = torch.empty_like(b)
wp_output = wp.from_torch(output)
with wp.Tape() as tape:
wp.launch(
kernel=forward_kernel,
dim=(N),
device=device,
inputs=[
wp.from_torch(a),
wp.from_torch(b),
wp_output,
],
)
ctx.tape = tape
ctx.wp_output = wp_output
ctx.a = a
ctx.b = b
return output
@staticmethod
def backward(ctx, grad_output):
ctx.tape.backward(grads={ctx.wp_output: wp.from_torch(grad_output.contiguous())})
# Grab gradients before clearing references
grad_a = ctx.a.grad
grad_b = ctx.b.grad
# Clear context to break reference cycles and free memory
ctx.tape = None
ctx.wp_output = None
return grad_a, grad_b
This approach ensures gradients are allocated using PyTorch’s caching allocator, which properly tracks memory and stream dependencies. Pre-allocation can also be done earlier in the pipeline:
# At tensor creation time
a_torch = a.clone().detach().requires_grad_(True)
b_torch = b.clone().detach().requires_grad_(True)
# Pre-allocate gradients immediately
a_torch.grad = torch.empty_like(a_torch)
b_torch.grad = torch.empty_like(b_torch)
# Now safe to use in WarpFunction
output = WarpFunction.apply(a_torch, b_torch)
Performance Comparison#
Benchmarking these approaches on a workload with N=300,000,000 elements shows:
Baseline (with synchronization overhead): 98.02 ms
Solution A (requires_grad=False): 22.59 ms (4.3x faster)
Solution B (detach): 22.11 ms (4.4x faster)
Solution C (pre-allocate): 28.62 ms (3.4x faster)
All three solutions eliminate the synchronization overhead:
Solutions A and B are fastest because they allocate gradients in the backward pass as simple standalone tensors
Solution C is slightly slower because it allocates gradients in the forward pass and attaches them as
.gradattributes, which involves PyTorch’s autograd bookkeeping
Choose based on your workflow:
Solution A: Most explicit about disabling gradient tracking
Solution B: Cleanest for manual gradient management
Solution C: Required when using Warp’s tape or when you need
.gradaccess
These solutions are primarily needed when working with newly created tensors in scenarios like:
Training loops that create fresh tensors each iteration
Repeated inference with dynamically allocated tensors
Any workflow using
.clone().detach().requires_grad_(True)patterns
If you recycle the same tensors across iterations (whose gradients have already been allocated), there will be no need for gradient allocation (deferred or otherwise) and therefore no synchronization overhead.
CuPy/Numba#
Warp GPU arrays support the __cuda_array_interface__ protocol for sharing data with other Python GPU frameworks.
This allows frameworks like CuPy to use Warp GPU arrays directly.
Likewise, Warp arrays can be created from any object that exposes the __cuda_array_interface__.
Such objects can also be passed to Warp kernels directly without creating a Warp array object.
JAX#
Interoperability with JAX arrays is supported through the following methods. Internally these use the DLPack protocol to exchange data in a zero-copy way with JAX:
warp_array = wp.from_jax(jax_array)
jax_array = wp.to_jax(warp_array)
It may be preferable to use the DLPack protocol directly for better performance and control over stream synchronization .
- warp.from_jax(jax_array, dtype=None)[source]#
Convert a Jax array to a Warp array without copying the data.
- Parameters:
jax_array (jax.Array) – The Jax array to convert.
dtype (optional) – The target data type of the resulting Warp array. Defaults to the Jax array’s data type mapped to a Warp data type.
- Returns:
The converted Warp array.
- Return type:
- warp.to_jax(warp_array)[source]#
Convert a Warp array to a Jax array without copying the data.
- Parameters:
warp_array (warp.array) – The Warp array to convert.
- Returns:
The converted Jax array.
- Return type:
- warp.device_from_jax(jax_device)[source]#
Return the Warp device corresponding to a Jax device.
- Parameters:
jax_device (jax.Device) – A Jax device descriptor.
- Raises:
RuntimeError – The Jax device is neither a CPU nor GPU device.
- Return type:
- warp.device_to_jax(warp_device)[source]#
Return the Jax device corresponding to a Warp device.
- Returns:
- Raises:
RuntimeError – Failed to find the corresponding Jax device.
- Parameters:
- warp.dtype_from_jax(jax_dtype)[source]#
Return the Warp dtype corresponding to a Jax dtype.
- Raises:
TypeError – Unable to find a corresponding Warp data type.
- warp.dtype_to_jax(warp_dtype)[source]#
Return the Jax dtype corresponding to a Warp dtype.
- Parameters:
warp_dtype – A Warp data type that has a corresponding Jax data type.
- Raises:
TypeError – Unable to find a corresponding Jax data type.
Using Warp kernels as JAX primitives#
Warp kernels can be used as JAX primitives, which allows calling them inside of jitted JAX functions:
import warp as wp
import jax
import jax.numpy as jnp
from warp.jax_experimental import jax_kernel
@wp.kernel
def triple_kernel(input: wp.array(dtype=float), output: wp.array(dtype=float)):
tid = wp.tid()
output[tid] = 3.0 * input[tid]
# create a Jax primitive from a Warp kernel
jax_triple = jax_kernel(triple_kernel)
# use the Warp kernel in a Jax jitted function
@jax.jit
def f():
x = jnp.arange(0, 64, dtype=jnp.float32)
return jax_triple(x)
print(f())
- warp.jax_experimental.jax_kernel(
- kernel,
- num_outputs=1,
- vmap_method='broadcast_all',
- launch_dims=None,
- output_dims=None,
- in_out_argnames=None,
- module_preload_mode=ModulePreloadMode.CURRENT_DEVICE,
- enable_backward=False,
Create a JAX callback from a Warp kernel.
NOTE: This is an experimental feature under development.
- Parameters:
kernel – The Warp kernel to launch.
num_outputs – Specify the number of output arguments if greater than 1. This must include the number of
in_out_arguments.vmap_method – String specifying how the callback transforms under
vmap(). This argument can also be specified for individual calls.launch_dims – Specify the default kernel launch dimensions. If None, launch dimensions are inferred from the shape of the first array argument. This argument can also be specified for individual calls.
output_dims – Specify the default dimensions of output arrays. If None, output dimensions are inferred from the launch dimensions. This argument can also be specified for individual calls.
in_out_argnames – Names of arguments that are both inputs and outputs (aliased buffers). These must be array arguments that appear before any pure output arguments in the kernel signature. The number of in-out arguments is included in
num_outputs. Not supported whenenable_backward=True.module_preload_mode – Specify the devices where the module should be preloaded.
enable_backward (bool) – Enable automatic differentiation for this kernel.
- Limitations:
All kernel arguments must be contiguous arrays or scalars.
Scalars must be static arguments in JAX.
Input and input-output arguments must precede the output arguments in the
kerneldefinition.There must be at least one output or input-output argument.
Only the CUDA backend is supported.
Input and Output Semantics#
Input arguments must come before output arguments in the kernel definition.
At least one output array is required, but it’s ok to have kernels with no inputs.
The number of outputs can be specified using the num_outputs argument, which defaults to one.
Here’s a kernel with two inputs and one output:
import jax
import jax.numpy as jnp
import warp as wp
from warp.jax_experimental import jax_kernel
@wp.kernel
def add_kernel(a: wp.array(dtype=int),
b: wp.array(dtype=int),
output: wp.array(dtype=int)):
tid = wp.tid()
output[tid] = a[tid] + b[tid]
jax_add = jax_kernel(add_kernel)
@jax.jit
def f():
n = 10
a = jnp.arange(n, dtype=jnp.int32)
b = jnp.ones(n, dtype=jnp.int32)
return jax_add(a, b)
print(f())
One input and two outputs:
import math
import jax
import jax.numpy as jnp
import warp as wp
from warp.jax_experimental import jax_kernel
@wp.kernel
def sincos_kernel(angle: wp.array(dtype=float),
# outputs
sin_out: wp.array(dtype=float),
cos_out: wp.array(dtype=float)):
tid = wp.tid()
sin_out[tid] = wp.sin(angle[tid])
cos_out[tid] = wp.cos(angle[tid])
jax_sincos = jax_kernel(sincos_kernel, num_outputs=2) # specify multiple outputs
@jax.jit
def f():
a = jnp.linspace(0, 2 * math.pi, 32)
return jax_sincos(a)
s, c = f()
print(s)
print(c)
Here is a kernel with no inputs that initializes an array of 3x3 matrices with the diagonal values (1, 2, 3). With no inputs, specifying the launch dimensions is required to determine the shape of the output array:
@wp.kernel
def diagonal_kernel(output: wp.array(dtype=wp.mat33)):
tid = wp.tid()
output[tid] = wp.mat33(1.0, 0.0, 0.0, 0.0, 2.0, 0.0, 0.0, 0.0, 3.0)
jax_diagonal = jax_kernel(diagonal_kernel)
@jax.jit
def f():
# launch dimensions determine the output shape
return jax_diagonal(launch_dims=4)
print(f())
Scalar Inputs#
Scalar input arguments are supported, although there are some limitations. Currently, scalars passed to Warp kernels must be constant or static values in JAX:
@wp.kernel
def scale_kernel(a: wp.array(dtype=float),
s: float, # scalar input
output: wp.array(dtype=float)):
tid = wp.tid()
output[tid] = a[tid] * s
jax_scale = jax_kernel(scale_kernel)
@jax.jit
def f():
a = jnp.arange(10, dtype=jnp.float32)
return jax_scale(a, 2.0) # ok: constant scalar argument
print(f())
Trying to use a traced scalar value will result in an exception:
@jax.jit
def f(a, s):
return jax_scale(a, s) # ERROR: traced scalar argument
a = jnp.arange(10, dtype=jnp.float32)
print(f(a, 2.0))
JAX static arguments to the rescue:
# make scalar arguments static
@partial(jax.jit, static_argnames=["s"])
def f(a, s):
return jax_scale(a, s) # ok: static scalar argument
a = jnp.arange(10, dtype=jnp.float32)
print(f(a, 2.0))
Kernel Launch and Output Dimensions#
By default, the launch dimensions are inferred from the shape of the first input array.
When that’s not appropriate, the launch_dims argument can be used to override this behavior.
The launch dimensions also determine the shape of the output arrays.
Here is a simple matrix multiplication kernel that multiplies an NxK matrix by a KxM matrix. The launch dimensions and output shape must be (N, M), which is different than the shape of the input arrays:
@wp.kernel
def matmul_kernel(
a: wp.array2d(dtype=float), # NxK input
b: wp.array2d(dtype=float), # KxM input
c: wp.array2d(dtype=float), # NxM output
):
# launch dimensions should be (N, M)
i, j = wp.tid()
N = a.shape[0]
K = a.shape[1]
M = b.shape[1]
if i < N and j < M:
s = wp.float32(0)
for k in range(K):
s += a[i, k] * b[k, j]
c[i, j] = s
# no need to specify launch dims here
jax_matmul = jax_kernel(matmul_kernel)
@jax.jit
def f():
N1, M1, K1 = 3, 4, 2
a1 = jnp.full((N1, K1), 2, dtype=jnp.float32)
b1 = jnp.full((K1, M1), 3, dtype=jnp.float32)
# use custom launch dims
result1 = jax_matmul(a1, b1, launch_dims=(N1, M1))
N2, M2, K2 = 4, 3, 2
a2 = jnp.full((N2, K2), 2, dtype=jnp.float32)
b2 = jnp.full((K2, M2), 3, dtype=jnp.float32)
# use custom launch dims
result2 = jax_matmul(a2, b2, launch_dims=(N2, M2))
return result1, result2
r1, r2 = f()
print(r1)
print(r2)
By default, output array shapes are determined from the launch dimensions, but it’s possible to specify custom output
dimensions using the output_dims argument. Consider a kernel like this:
@wp.kernel
def funky_kernel(a: wp.array(dtype=float),
# outputs
b: wp.array(dtype=float),
c: wp.array(dtype=float)):
...
jax_funky = jax_kernel(funky_kernel, num_outputs=2)
Specify a custom output shape used for all outputs:
b, c = jax_funky(a, output_dims=n)
Specify different output dimensions for each output using a dictionary:
b, c = jax_funky(a, output_dims={"b": n, "c": m})
Specify custom launch and output dimensions together:
b, c = jax_funky(a, launch_dims=k, output_dims={"b": n, "c": m})
One-dimensional shapes can be specified using an integer. Multi-dimensional shapes can be specified using tuples or lists of integers.
Vector and Matrix Arrays#
Arrays of Warp vector and matrix types are supported.
Since JAX does not have corresponding data types, the components are packed into extra inner dimensions of JAX arrays.
For example, a Warp array of wp.vec3 will have a JAX array shape of (…, 3) and a Warp array of wp.mat22 will
have a JAX array shape of (…, 2, 2):
@wp.kernel
def vecmat_kernel(a: wp.array(dtype=float),
b: wp.array(dtype=wp.vec3),
c: wp.array(dtype=wp.mat22),
# outputs
d: wp.array(dtype=float),
e: wp.array(dtype=wp.vec3),
f: wp.array(dtype=wp.mat22)):
...
jax_vecmat = jax_kernel(vecmat_kernel, num_outputs=3)
@jax.jit
def f():
n = 10
a = jnp.zeros(n, dtype=jnp.float32) # scalar array
b = jnp.zeros((n, 3), dtype=jnp.float32) # vec3 array
c = jnp.zeros((n, 2, 2), dtype=jnp.float32) # mat22 array
d, e, f = vecmat_kernel(a, b, c)
It’s important to recognize that the Warp and JAX array shapes are different for vector and matrix types.
In the above snippet, Warp sees a, b, and c as one-dimensional arrays of wp.float32, wp.vec3, and
wp.mat22, respectively. In JAX, a is a one-dimensional array with length n, b is a two-dimensional array
with shape (n, 3), and c is a three-dimensional array with shape (n, 2, 2).
When specifying custom output dimensions, it’s possible to use either convention. The following calls are equivalent:
d, e, f = vecmat_kernel(a, b, c, output_dims=n)
d, e, f = vecmat_kernel(a, b, c, output_dims={"d": n, "e": n, "f": n})
d, e, f = vecmat_kernel(a, b, c, output_dims={"d": n, "e": (n, 3), "f": (n, 2, 2)})
This is a convenience feature meant to simplify writing code. For example, when Warp expects the arrays to be of the same shape, we only need to specify the shape once without worrying about the extra vector and matrix dimensions required by JAX:
d, e, f = vecmat_kernel(a, b, c, output_dims=n)
On the other hand, JAX dimensions are also accepted to allow passing shapes directly from JAX:
d, e, f = vecmat_kernel(a, b, c, output_dims={"d": a.shape, "e": b.shape, "f": c.shape})
See example_jax_kernel.py for examples.
JAX VMAP Support#
The vmap_method argument can be used to specify how the callback transforms under jax.vmap().
The default is "broadcast_all". This argument can be passed to jax_kernel(),
and it can also be passed to each call:
# set default vmap behavior
jax_callback = jax_kernel(my_kernel, vmap_method="sequential")
@jax.jit
def f():
...
b = jax_callback(a) # uses "sequential"
...
d = jax_callback(c, vmap_method="expand_dims") # uses "expand_dims"
...
JAX Automatic Differentiation#
Warp kernels can be given JAX gradients using a convenience wrapper that wires a custom VJP around a kernel and its adjoint. To enable autodiff, pass the enable_backward=True argument to jax_kernel().
Basic example (one output):
from functools import partial
import jax
import jax.numpy as jnp
import warp as wp
from warp.jax_experimental import jax_kernel
@wp.kernel
def scale_sum_square(
a: wp.array(dtype=float),
b: wp.array(dtype=float),
s: float,
out: wp.array(dtype=float),
):
tid = wp.tid()
out[tid] = (a[tid] * s + b[tid]) ** 2.0
jax_scale = jax_kernel(scale_sum_square, num_outputs=1, enable_backward=True)
# scalars must be static
@partial(jax.jit, static_argnames=["s"])
def loss(a, b, s):
(out,) = jax_scale(a, b, s)
return jnp.sum(out)
n = 16
a = jnp.arange(n, dtype=jnp.float32)
b = jnp.ones(n, dtype=jnp.float32)
s = 2.0
# gradients w.r.t. array inputs
da, db = jax.grad(loss, argnums=(0, 1))(a, b, s)
print(da)
print(db)
Multiple outputs:
import jax
import jax.numpy as jnp
import warp as wp
from warp.jax_experimental import jax_kernel
@wp.kernel
def multi_output(
a: wp.array(dtype=float),
b: wp.array(dtype=float),
s: float,
c: wp.array(dtype=float),
d: wp.array(dtype=float),
):
tid = wp.tid()
c[tid] = a[tid] ** 2.0
d[tid] = a[tid] * b[tid] * s
jax_multi = jax_kernel(multi_output, num_outputs=2, enable_backward=True)
def caller(fn, a, b, s):
c, d = fn(a, b, s)
return jnp.sum(c + d)
n = 16
a = jnp.arange(n, dtype=jnp.float32)
b = jnp.ones(n, dtype=jnp.float32)
s = 2.0
# differentiate a batched scalar objective over two inputs
da, db = jax.grad(lambda a, b, s: caller(jax_multi, a, b, s), argnums=(0, 1))(a, b, s)
print(da)
print(db)
Vector and matrix arrays also work. Inner component dimensions are packed in the JAX array and handled automatically:
from functools import partial
import jax
import jax.numpy as jnp
import warp as wp
from warp.jax_experimental import jax_kernel
@wp.kernel
def scale_vec2(a: wp.array(dtype=wp.vec2), s: float, out: wp.array(dtype=wp.vec2)):
tid = wp.tid()
out[tid] = a[tid] * s
jax_vec = jax_kernel(scale_vec2, num_outputs=1, enable_backward=True)
@partial(jax.jit, static_argnames=["s"])
def vec_loss(a, s):
(out,) = jax_vec(a, s)
return jnp.sum(out)
a2 = jnp.arange(10, dtype=jnp.float32).reshape((5, 2)) # vec2 payload shape
(da2,) = jax.grad(vec_loss, argnums=(0,))(a2, 3.0)
print(da2)
Limitations#
The autodiff functionality is considered experimental and is still a work in progress.
Scalar inputs must be static arguments in JAX.
Gradients are returned for differentiable array inputs (static scalars are excluded from the gradient tuple).
Input-output arguments (
in_out_argnames) are not supported whenenable_backward=True, because in-place modifications are not differentiable.Custom launch and output dimensions (
launch_dims,output_dims) are not currently supported whenenable_backward=True, but the goal is to support them in the future. Launch dimensions are inferred from the shape of the first array argument, thus at least one input array is required.
Calling Annotated Python Functions#
The jax_kernel() mechanism can be used to launch a single Warp kernel
from JAX, but it’s also possible to call a Python function that launches multiple kernels.
The target Python function should have argument type annotations as if it were a Warp kernel.
To call this function from JAX, use jax_callable():
from warp.jax_experimental import jax_callable
@wp.kernel
def scale_kernel(a: wp.array(dtype=float), s: float, output: wp.array(dtype=float)):
tid = wp.tid()
output[tid] = a[tid] * s
@wp.kernel
def scale_vec_kernel(a: wp.array(dtype=wp.vec2), s: float, output: wp.array(dtype=wp.vec2)):
tid = wp.tid()
output[tid] = a[tid] * s
# The Python function to call.
# Note the argument type annotations, just like Warp kernels.
def example_func(
# inputs
a: wp.array(dtype=float),
b: wp.array(dtype=wp.vec2),
s: float,
# outputs
c: wp.array(dtype=float),
d: wp.array(dtype=wp.vec2),
):
# launch multiple kernels
wp.launch(scale_kernel, dim=a.shape, inputs=[a, s], outputs=[c])
wp.launch(scale_vec_kernel, dim=b.shape, inputs=[b, s], outputs=[d])
jax_func = jax_callable(example_func, num_outputs=2)
@jax.jit
def f():
# inputs
a = jnp.arange(10, dtype=jnp.float32)
b = jnp.arange(10, dtype=jnp.float32).reshape((5, 2)) # wp.vec2
s = 2.0
# output shapes
output_dims = {"c": a.shape, "d": b.shape}
c, d = jax_func(a, b, s, output_dims=output_dims)
return c, d
r1, r2 = f()
print(r1)
print(r2)
The input and output semantics of jax_callable() are similar to
jax_kernel(), so we won’t recap everything here,
just focus on the differences:
jax_callable()does not take alaunch_dimsargument, since the target function is responsible for launching kernels using appropriate dimensions.jax_callable()takes an optionalgraph_modeargument, which determines how the callable can be captured in a CUDA graph. Graphs are generally desirable, since they can greatly improve the application performance.GraphMode.JAX(default) lets JAX capture the graph, which may be used as a subgraph in an enclosing capture for maximal benefit.GraphMode.WARPlets Warp capture the graph. Use this mode when the callable cannot be used as a subgraph, such as when the callable uses conditional graph nodes.GraphMode.NONEdisables graph capture. Use this mode if the callable performs operations that are not allowed during graph capture, such as host synchronization.
See example_jax_callable.py for examples.
- warp.jax_experimental.jax_callable(
- func,
- num_outputs=1,
- graph_compatible=None,
- graph_mode=GraphMode.JAX,
- vmap_method='broadcast_all',
- output_dims=None,
- in_out_argnames=None,
- graph_cache_max=None,
- module_preload_mode=ModulePreloadMode.CURRENT_DEVICE,
Create a JAX callback from an annotated Python function.
The Python function arguments must have type annotations like Warp kernels.
NOTE: This is an experimental feature under development.
- Parameters:
func (Callable) – The Python function to call.
num_outputs (int) – Specify the number of output arguments if greater than 1. This must include the number of
in_out_arguments.graph_compatible (bool | None) – Whether the function can be called during CUDA graph capture. This argument is deprecated, use
graph_modeinstead.graph_mode (GraphMode) – CUDA graph capture mode.
GraphMode.JAX(default): Let JAX capture the graph, which may be used as a subgraph in an enclosing JAX capture.GraphMode.WARP: Let Warp capture the graph. Use this mode when the callable cannot be used as a subgraph, such as when the callable uses conditional graph nodes.GraphMode.NONE: Disable graph capture. Use when the callable performs operations that are not legal in a graph, such as host synchronization.vmap_method (str | None) – String specifying how the callback transforms under
vmap(). This argument can also be specified for individual calls.output_dims – Specify the default dimensions of output arrays. If
None, output dimensions are inferred from the launch dimensions. This argument can also be specified for individual calls.in_out_argnames – Names of arguments that are both inputs and outputs (aliased buffers). These must be array arguments that appear before any pure output arguments in the function signature. The number of in-out arguments is included in
num_outputs.graph_cache_max (int | None) – Maximum number of cached graphs captured using
GraphMode.WARP. IfNone, usewarp.jax_experimental.get_jax_callable_default_graph_cache_max().module_preload_mode (ModulePreloadMode) – Specify the devices where the module should be preloaded.
- Limitations:
All kernel arguments must be contiguous arrays or scalars.
Scalars must be static arguments in JAX.
Input and input-output arguments must precede the output arguments in the
funcdefinition.There must be at least one output or input-output argument.
Only the CUDA backend is supported.
Generic JAX FFI Callbacks#
Another way to call Python functions is to use
register_ffi_callback():
from warp.jax_experimental import register_ffi_callback
This allows calling functions that don’t have Warp-style type annotations, but must have the form:
func(inputs, outputs, attrs, ctx)
where:
inputsis a list of input buffers.outputsis a list of output buffers.attrsis a dictionary of attributes.ctxis the execution context, including the CUDA stream.
The input and output buffers are neither JAX nor Warp arrays.
They are objects that expose the __cuda_array_interface__, which can be passed to Warp kernels directly.
Here is an example:
from warp.jax_experimental import register_ffi_callback
@wp.kernel
def scale_kernel(a: wp.array(dtype=float), s: float, output: wp.array(dtype=float)):
tid = wp.tid()
output[tid] = a[tid] * s
@wp.kernel
def scale_vec_kernel(a: wp.array(dtype=wp.vec2), s: float, output: wp.array(dtype=wp.vec2)):
tid = wp.tid()
output[tid] = a[tid] * s
# the Python function to call
def warp_func(inputs, outputs, attrs, ctx):
# input arrays
a = inputs[0]
b = inputs[1]
# scalar attributes
s = attrs["scale"]
# output arrays
c = outputs[0]
d = outputs[1]
device = wp.device_from_jax(get_jax_device())
stream = wp.Stream(device, cuda_stream=ctx.stream)
with wp.ScopedStream(stream):
# launch with arrays of scalars
wp.launch(scale_kernel, dim=a.shape, inputs=[a, s], outputs=[c])
# launch with arrays of vec2
# NOTE: the input shapes are from JAX arrays, so we need to strip the inner dimension for vec2 arrays
wp.launch(scale_vec_kernel, dim=b.shape[0], inputs=[b, s], outputs=[d])
# register callback
register_ffi_callback("warp_func", warp_func)
n = 10
# inputs
a = jnp.arange(n, dtype=jnp.float32)
b = jnp.arange(n, dtype=jnp.float32).reshape((n // 2, 2)) # array of wp.vec2
s = 2.0
# set up the call
out_types = [
jax.ShapeDtypeStruct(a.shape, jnp.float32),
jax.ShapeDtypeStruct(b.shape, jnp.float32), # array of wp.vec2
]
call = jax.ffi.ffi_call("warp_func", out_types)
# call it
c, d = call(a, b, scale=s)
print(c)
print(d)
This is a more low-level approach to JAX FFI callbacks.
A proposal was made to incorporate such a mechanism in JAX, but for now we have a prototype here.
This approach leaves a lot of work up to the user, such as verifying argument types and shapes,
but it can be used when other utilities like jax_kernel() and
jax_callable() are not sufficient.
See example_jax_ffi_callback.py for examples.
Distributed Computation#
Warp can be used in conjunction with JAX’s shard_map to perform distributed multi-GPU computations.
To achieve this, the JAX distributed environment must be initialized (see Distributed Arrays and Automatic Parallelization for more details):
import jax
jax.distributed.initialize()
This initialization must be called at the beginning of your program, before any other JAX operations.
Here’s an example of how to use shard_map with a Warp kernel:
import warp as wp
import jax
import jax.numpy as jnp
from jax.sharding import PartitionSpec as P
from jax.experimental.multihost_utils import process_allgather as allgather
from jax.experimental.shard_map import shard_map
from warp.jax_experimental import jax_kernel
import numpy as np
# Initialize JAX distributed environment
jax.distributed.initialize()
num_gpus = jax.device_count()
def print_on_process_0(*args, **kwargs):
if jax.process_index() == 0:
print(*args, **kwargs)
print_on_process_0(f"Running on {num_gpus} GPU(s)")
@wp.kernel
def multiply_by_two_kernel(
a_in: wp.array(dtype=wp.float32),
a_out: wp.array(dtype=wp.float32),
):
index = wp.tid()
a_out[index] = a_in[index] * 2.0
jax_warp_multiply = jax_kernel(multiply_by_two_kernel)
def warp_multiply(x):
result = jax_warp_multiply(x)
return result
# a_in here is the full sharded array with shape (M,)
# The output will also be a sharded array with shape (M,)
def warp_distributed_operator(a_in):
def _sharded_operator(a_in):
# Inside the sharded operator, a_in is a local shard on each device
# If we have N devices and input size M, each shard has shape (M/N,)
# warp_multiply applies the Warp kernel to the local shard
result = warp_multiply(a_in)[0]
# result has the same shape as the input shard (M/N,)
return result
# shard_map distributes the computation across devices
return shard_map(
_sharded_operator,
mesh=jax.sharding.Mesh(np.array(jax.devices()), "x"),
in_specs=(P("x"),), # Input is sharded along the 'x' axis
out_specs=P("x"), # Output is also sharded along the 'x' axis
check_rep=False,
)(a_in)
print_on_process_0("Test distributed multiplication using JAX + Warp")
devices = jax.devices()
mesh = jax.sharding.Mesh(np.array(devices), "x")
sharding_spec = jax.sharding.NamedSharding(mesh, P("x"))
input_size = num_gpus * 5 # 5 elements per device
single_device_arrays = jnp.arange(input_size, dtype=jnp.float32)
# Define the shape of the input array based on the total input size
shape = (input_size,)
# Create a list of arrays by distributing the single_device_arrays across the available devices
# Each device will receive a portion of the input data
arrays = [
jax.device_put(single_device_arrays[index], d) # Place each element on the corresponding device
for d, index in sharding_spec.addressable_devices_indices_map(shape).items()
]
# Combine the individual device arrays into a single sharded array
sharded_array = jax.make_array_from_single_device_arrays(shape, sharding_spec, arrays)
# sharded_array has shape (input_size,) but is distributed across devices
print_on_process_0(f"Input array: {allgather(sharded_array)}")
# warp_result has the same shape and sharding as sharded_array
warp_result = warp_distributed_operator(sharded_array)
# allgather collects results from all devices, resulting in a full array of shape (input_size,)
print_on_process_0("Warp Output:", allgather(warp_result))
In this example, shard_map is used to distribute the computation across available devices.
The input array a_in is sharded along the ‘x’ axis, and each device processes its local shard.
The Warp kernel multiply_by_two_kernel is applied to each shard, and the results are combined to form the final output.
This approach allows for efficient parallel processing of large arrays, as each device works on a portion of the data simultaneously.
To run this program on multiple GPUs, you must have Open MPI installed.
You can consult the OpenMPI installation guide
for instructions on how to install it.
Once Open MPI is installed, you can use mpirun with the following command:
mpirun -np <NUM_OF_GPUS> python <filename>.py
DLPack#
Warp supports the DLPack protocol included in the Python Array API standard v2022.12. See the Python Specification for DLPack for reference.
The canonical way to import an external array into Warp is using the warp.from_dlpack() function:
warp_array = wp.from_dlpack(external_array)
The external array can be a PyTorch tensor, Jax array, or any other array type compatible with this version of the DLPack protocol.
For CUDA arrays, this approach requires the producer to perform stream synchronization which ensures that operations on the array
are ordered correctly. The warp.from_dlpack() function asks the producer to synchronize the current Warp stream on the device where
the array resides. Thus it should be safe to use the array in Warp kernels on that device without any additional synchronization.
The canonical way to export a Warp array to an external framework is to use the from_dlpack() function in that framework:
jax_array = jax.dlpack.from_dlpack(warp_array)
torch_tensor = torch.utils.dlpack.from_dlpack(warp_array)
paddle_tensor = paddle.utils.dlpack.from_dlpack(warp_array)
For CUDA arrays, this will synchronize the current stream of the consumer framework with the current Warp stream on the array’s device. Thus it should be safe to use the wrapped array in the consumer framework, even if the array was previously used in a Warp kernel on the device.
Alternatively, arrays can be shared by explicitly creating PyCapsules using a to_dlpack() function provided by the producer framework.
This approach may be used for older versions of frameworks that do not support the v2022.12 standard:
warp_array1 = wp.from_dlpack(jax_array)
warp_array2 = wp.from_dlpack(torch.utils.dlpack.to_dlpack(torch_tensor))
warp_array3 = wp.from_dlpack(paddle.utils.dlpack.to_dlpack(paddle_tensor))
jax_array = jax.dlpack.from_dlpack(wp.to_dlpack(warp_array))
torch_tensor = torch.utils.dlpack.from_dlpack(wp.to_dlpack(warp_array))
paddle_tensor = paddle.utils.dlpack.from_dlpack(wp.to_dlpack(warp_array))
This approach is generally faster because it skips any stream synchronization, but another solution must be used to ensure correct ordering of operations. In situations where no synchronization is required, using this approach can yield better performance. This may be a good choice in situations like these:
The external framework is using the synchronous CUDA default stream.
Warp and the external framework are using the same CUDA stream.
Another synchronization mechanism is already in place.
- warp.from_dlpack(source, dtype=None)[source]#
Convert a source array or DLPack capsule into a Warp array without copying.
- Parameters:
source – A DLPack-compatible array or PyCapsule
dtype – An optional Warp data type to interpret the source data.
- Returns:
A new Warp array that uses the same underlying memory as the input pycapsule.
- Return type:
- warp.to_dlpack(wp_array)[source]#
Convert a Warp array to another type of DLPack-compatible array.
- Parameters:
wp_array (array) – The source Warp array that will be converted.
- Returns:
A capsule containing a DLManagedTensor that can be converted to another array type without copying the underlying memory.
Paddle#
Warp provides helper functions to convert arrays to/from Paddle:
w = wp.array([1.0, 2.0, 3.0], dtype=float, device="cpu")
# convert to Paddle tensor
t = wp.to_paddle(w)
# convert from Paddle tensor
w = wp.from_paddle(t)
These helper functions allow the conversion of Warp arrays to/from Paddle tensors without copying the underlying data. At the same time, if available, gradient arrays and tensors are converted to/from Paddle autograd tensors, allowing the use of Warp arrays in Paddle autograd computations.
- warp.from_paddle(
- t,
- dtype=None,
- requires_grad=None,
- grad=None,
- return_ctype=False,
Convert a Paddle tensor to a Warp array without copying the data.
- Parameters:
t (paddle.Tensor) – The paddle tensor to wrap.
dtype (warp.dtype, optional) – The target data type of the resulting Warp array. Defaults to the tensor value type mapped to a Warp array value type.
requires_grad (bool, optional) – Whether the resulting array should wrap the tensor’s gradient, if it exists (the grad tensor will be allocated otherwise). Defaults to the tensor’s requires_grad value.
grad (paddle.Tensor, optional) – The grad attached to given tensor. Defaults to None.
return_ctype (bool, optional) – Whether to return a low-level array descriptor instead of a
wp.arrayobject (faster). The descriptor can be passed to Warp kernels.
- Returns:
The wrapped array or array descriptor.
- Return type:
- warp.to_paddle(a, requires_grad=None)[source]#
Convert a Warp array to a Paddle tensor without copying the data.
- Parameters:
a (warp.array) – The Warp array to convert.
requires_grad (bool, optional) – Whether the resulting tensor should convert the array’s gradient, if it exists, to a grad tensor. Defaults to the array’s requires_grad value.
- Returns:
The converted tensor.
- Return type:
paddle.Tensor
- warp.device_from_paddle(paddle_device)[source]#
Return the Warp device corresponding to a Paddle device.
- Parameters:
paddle_device (Place, CPUPlace, CUDAPinnedPlace, CUDAPlace, or str) – Paddle device identifier
- Raises:
RuntimeError – Paddle device does not have a corresponding Warp device
- Return type:
- warp.device_to_paddle(warp_device)[source]#
Return the Paddle device string corresponding to a Warp device.
- Parameters:
warp_device (Device | str | None) – An identifier that can be resolved to a
warp._src.context.Device.- Raises:
RuntimeError – The Warp device is not compatible with PyPaddle.
- Return type:
- warp.dtype_from_paddle(paddle_dtype)[source]#
Return the Warp dtype corresponding to a Paddle dtype.
- Parameters:
paddle_dtype – A
paddle.dtypethat has a corresponding Warp data type. Currentlypaddle.bfloat16,paddle.complex64, andpaddle.complex128are not supported.- Raises:
TypeError – Unable to find a corresponding Warp data type.
- warp.dtype_to_paddle(warp_dtype)[source]#
Return the Paddle dtype corresponding to a Warp dtype.
- Parameters:
warp_dtype – A Warp data type that has a corresponding
paddle.dtype.warp.uint16,warp.uint32, andwarp.uint64are mapped to the signed integerpaddle.dtypeof the same width.- Raises:
TypeError – Unable to find a corresponding PyPaddle data type.
To convert a Paddle CUDA stream to a Warp CUDA stream and vice versa, Warp provides the following function:
- warp.stream_from_paddle(stream_or_device=None)[source]#
Convert from a Paddle CUDA stream to a Warp CUDA stream.
Example: Optimization using warp.from_paddle()#
An example usage of minimizing a loss function over an array of 2D points written in Warp via Paddle’s Adam optimizer
using warp.from_paddle() is as follows:
import warp as wp
import paddle
# init warp context at beginning
wp.init()
@wp.kernel()
def loss(xs: wp.array(dtype=float, ndim=2), l: wp.array(dtype=float)):
tid = wp.tid()
wp.atomic_add(l, 0, xs[tid, 0] ** 2.0 + xs[tid, 1] ** 2.0)
# indicate requires_grad so that Warp can accumulate gradients in the grad buffers
xs = paddle.randn([100, 2])
xs.stop_gradient = False
l = paddle.zeros([1])
l.stop_gradient = False
opt = paddle.optimizer.Adam(learning_rate=0.1, parameters=[xs])
wp_xs = wp.from_paddle(xs)
wp_l = wp.from_paddle(l)
tape = wp.Tape()
with tape:
# record the loss function kernel launch on the tape
wp.launch(loss, dim=len(xs), inputs=[wp_xs], outputs=[wp_l], device=wp_xs.device)
for i in range(500):
tape.zero()
tape.backward(loss=wp_l) # compute gradients
# now xs.grad will be populated with the gradients computed by Warp
opt.step() # update xs (and thereby wp_xs)
# these lines are only needed for evaluating the loss
# (the optimization just needs the gradient, not the loss value)
wp_l.zero_()
wp.launch(loss, dim=len(xs), inputs=[wp_xs], outputs=[wp_l], device=wp_xs.device)
print(f"{i}\tloss: {l.item()}")
Example: Optimization using warp.to_paddle#
Less code is needed when we declare the optimization variables directly in Warp and use warp.to_paddle() to convert them to Paddle tensors.
Here, we revisit the same example from above where now only a single conversion to a Paddle tensor is needed to supply Adam with the optimization variables:
import warp as wp
import numpy as np
import paddle
# init warp context at beginning
wp.init()
@wp.kernel()
def loss(xs: wp.array(dtype=float, ndim=2), l: wp.array(dtype=float)):
tid = wp.tid()
wp.atomic_add(l, 0, xs[tid, 0] ** 2.0 + xs[tid, 1] ** 2.0)
# initialize the optimization variables in Warp
xs = wp.array(np.random.randn(100, 2), dtype=wp.float32, requires_grad=True)
l = wp.zeros(1, dtype=wp.float32, requires_grad=True)
# just a single wp.to_paddle call is needed, Adam optimizes using the Warp array gradients
opt = paddle.optimizer.Adam(learning_rate=0.1, parameters=[wp.to_paddle(xs)])
tape = wp.Tape()
with tape:
wp.launch(loss, dim=len(xs), inputs=[xs], outputs=[l], device=xs.device)
for i in range(500):
tape.zero()
tape.backward(loss=l)
opt.step()
l.zero_()
wp.launch(loss, dim=len(xs), inputs=[xs], outputs=[l], device=xs.device)
print(f"{i}\tloss: {l.numpy()[0]}")
Performance Notes#
The wp.from_paddle() function creates a Warp array object that shares data with a Paddle tensor.
Although this function does not copy the data, there is always some CPU overhead during the conversion.
If these conversions happen frequently, the overall program performance may suffer.
As a general rule, it’s good to avoid repeated conversions of the same tensor.
Instead of:
x_t = paddle.arange(n, dtype=paddle.float32).to(device=wp.device_to_paddle(device))
y_t = paddle.ones([n], dtype=paddle.float32).to(device=wp.device_to_paddle(device))
for i in range(10):
x_w = wp.from_paddle(x_t)
y_w = wp.from_paddle(y_t)
wp.launch(saxpy, dim=n, inputs=[x_w, y_w, 1.0], device=device)
Try converting the arrays only once and reuse them:
x_t = paddle.arange(n, dtype=paddle.float32).to(device=wp.device_to_paddle(device))
y_t = paddle.ones([n], dtype=paddle.float32).to(device=wp.device_to_paddle(device))
x_w = wp.from_paddle(x_t)
y_w = wp.from_paddle(y_t)
for i in range(10):
wp.launch(saxpy, dim=n, inputs=[x_w, y_w, 1.0], device=device)
If reusing arrays is not possible (e.g., a new Paddle tensor is constructed on every iteration), passing return_ctype=True to
wp.from_paddle() should yield faster performance.
Setting this argument to True avoids constructing a wp.array object and instead returns a low-level array descriptor.
This descriptor is a simple C structure that can be passed to Warp kernels instead of a wp.array, but cannot be used in other places that require a wp.array.
for n in range(1, 10):
# get Paddle tensors for this iteration
x_t = paddle.arange(n, dtype=paddle.float32).to(device=wp.device_to_paddle(device))
y_t = paddle.ones([n], dtype=paddle.float32).to(device=wp.device_to_paddle(device))
# get Warp array descriptors
x_ctype = wp.from_paddle(x_t, return_ctype=True)
y_ctype = wp.from_paddle(y_t, return_ctype=True)
wp.launch(saxpy, dim=n, inputs=[x_ctype, y_ctype, 1.0], device=device)
An alternative approach is to pass the Paddle tensors to Warp kernels directly.
This avoids constructing temporary Warp arrays by leveraging standard array interfaces (like __cuda_array_interface__) supported by both Paddle and Warp.
The main advantage of this approach is convenience, since there is no need to call any conversion functions.
The main limitation is that it does not handle gradients, because gradient information is not included in the standard array interfaces.
This technique is therefore most suitable for algorithms that do not involve differentiation.
x = paddle.arange(n, dtype=paddle.float32).to(device=wp.device_to_paddle(device))
y = paddle.ones([n], dtype=paddle.float32).to(device=wp.device_to_paddle(device))
for i in range(10):
wp.launch(saxpy, dim=n, inputs=[x, y, 1.0], device=device)
python -m warp.examples.benchmarks.benchmark_interop_paddle
Sample output:
13990 ms from_paddle(...)
5990 ms from_paddle(..., return_ctype=True)
35167 ms direct from paddle
The default wp.from_paddle() conversion is the slowest.
Passing return_ctype=True is the fastest, because it skips creating temporary Warp array objects.
Passing Paddle tensors to Warp kernels directly falls somewhere in between.
It skips creating temporary Warp arrays, but accessing the __cuda_array_interface__ attributes of Paddle tensors adds overhead because they are initialized on-demand.