Quantum Volume

Quantum volume (QV) is a metric for determining the power of a noisy quantum device. The QV test is performed for a specified qubit number \(N\). If the test is passed, then the device can claim a quantum volume of \(2^N\). In practice, the procedure repeats, until the device reaches a qubit number for which the test fails and its greatest passing score is the device’s quantum volume. Though imperfect, the test is a reasonable approximation of the devices usable processing power. This tutorial will demonstrate how CUDA-Q can be used to perform the quantum volume test.

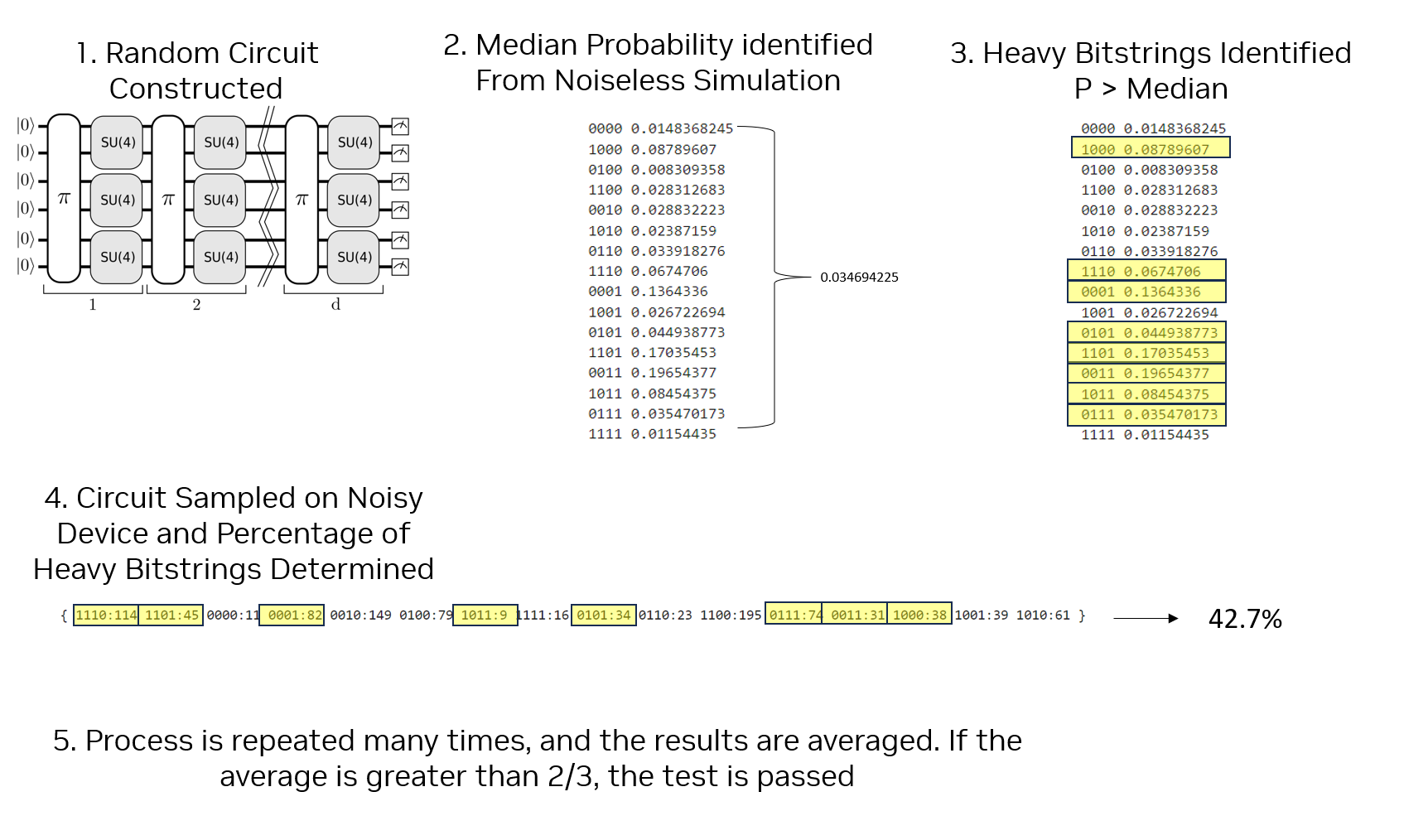
The test consists of the following steps (see figure below): 1. A special random circuit is constructed (details below) 2. A simulation determines the exact probability distribution of every bitstring and the median probability is determined. 3. Every bitstring which has an associated probability greater than the median, is considered a heavy bitstring for that particular circuit. 4. The circuit is sampled on the noisy device, and the percent of shots resulting in heavy bitstring are 5. The process is repeated many times and the resulted averaged. The test is passed if the average is greater than 2/3.

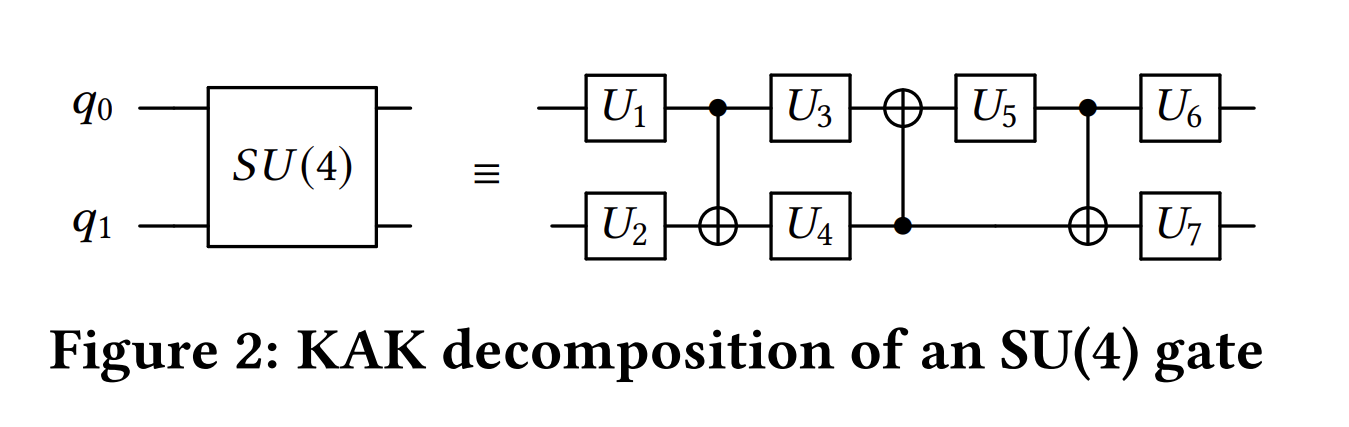
the circuits used are square, meaning they have the same number of layers as qubits. Each layer consists of a random permutation of qubits, followed by random SU4 operations applied to n/2 pairs of qubits. (See the first step in the figure above). For CUDA-Q implementation, the SU4 gates are decomposed using the KAK decomposition (figure from this paper).

The cell below specifies a circuit size n and two CUDA-Q kernels, one performing an SU4 operation and another building the entire QV circuit. This example is constructed for an even number of qubits for simplicity.

The QV kernel concludes with application of a bit flip operation on each qubit. This is not part of the QV circuit, but will be used later to introduce noise to the circuit. Otherwise the test would pass every time!

import cudaq
import numpy as np

# Select an even number
n = 4
su4_per_circuit = int(n / 2 * n)
n_params_in_su4 = 21


@cudaq.kernel
def su4_gate(q0: cudaq.qubit, q1: cudaq.qubit, params: list[float]):
    u3(params[0], params[1], params[2], q0)
    u3(params[3], params[4], params[5], q1)
    x.ctrl(q0, q1)
    u3(params[6], params[7], params[8], q0)
    u3(params[9], params[10], params[11], q1)
    x.ctrl(q1, q0)
    u3(params[12], params[13], params[14], q0)
    x.ctrl(q0, q1)
    u3(params[15], params[16], params[17], q0)
    u3(params[18], params[19], params[20], q0)


@cudaq.kernel
def qv(n: int, params: list[float], permutations: list[int]):

    reg = cudaq.qvector(n)
    param_index = 0

    for layer in range(n):
        for gate in range(n / 2):
            su4_gate(reg[permutations[layer * n + gate * 2]],
                     reg[permutations[layer * n + gate * 2 + 1]],
                     params[param_index:param_index + 21])
            param_index += 21

    x(reg)

Each circuit must be random. These function randomly choose parameters and permutations for each circuit.

def generate_random_params() -> list[float]:

    params = np.random.uniform(0, 2 * np.pi, n_params_in_su4 * su4_per_circuit)

    params_list = params.tolist()

    return params_list



def generate_random_permutations() -> list[int]:

    circuit_permutations = []

    for i in range(n):
        circuit_permutations.extend(
            np.random.permutation(n).astype(np.int64).tolist())

    return circuit_permutations


parameters = generate_random_params()
permutations = generate_random_permutations()

This function is an auxillary function used later to convert an integer into a “big endian” bitstring. This is used to help determine the heavy bitstrings.

def make_bitstring(integer) -> str:

    return bin(integer)[2:].zfill(n)[::-1]

The percent_heavy_sampled function takes the random circuit parameters and permutations and the error rate and returns the percent of heavy bitstrings produced by a noisy circuit sample.

The function first sets up the noise model. It assumes that each \(X\) gate applied at the end of the circuit will fail with some probability denoted by the error_rate.

Next, the noiseless simulation is performed on a GPU simulated with the nvidia backend to obtain the state vector. The density-matrix-cpu backend is used to sample the noisy circuit.

The rest of function processes these results to determine the heavy bitstring sample probabilities.

def percent_heavy_sampled(circuit_params,
                          layer_permutations,
                          error_rate,
                          print_output=False) -> float:

    # Includes option to print results for a single circuit

    # Define a bit flip error applied to all qubits
    noise = cudaq.NoiseModel()
    bf = cudaq.BitFlipChannel(error_rate)
    for i in range(n):
        noise.add_channel('x', [i], bf)

    # Gets noiseless probability distribution
    cudaq.set_target("nvidia")
    clean_result = np.array(
        cudaq.get_state(qv, n, circuit_params, layer_permutations))

    # Performs noisy sampling
    cudaq.set_target("density-matrix-cpu")
    noisy_result = cudaq.sample(qv,
                                n,
                                circuit_params,
                                layer_permutations,
                                noise_model=noise,
                                shots_count=1000)

    # Converts SV amplitudes to probabilities
    probs = clean_result * np.conjugate(clean_result)

    # Determines the median value
    cutoff = np.median(probs).real

    if print_output:
        print('The Median for this circuit is:')
        print(np.median(probs).real)

    # Determines if a bitstring is heavy and saves the bitstring in a list if so.
    heavy = []
    index = 0
    circuit_prob = 0

    for outcome_prob in probs:
        if outcome_prob.real > cutoff:
            heavy.append(make_bitstring(index))
            circuit_prob += outcome_prob.real
        index += 1

    if print_output:

        print('The heavy bitstrings for this circuit are')
        print(heavy)

        print('This circuit has an ideal havy sampling probability of:')
        print(circuit_prob)

    # Determines percent of noisy sample results that are heavy
    prob_heavy_in_noisy = 0
    for heavy_bitstring in heavy:
        prob_heavy_in_noisy += noisy_result.probability(heavy_bitstring)

    if print_output:
        print('Percent of time noisy sample returned heavy bitstring')
        print(prob_heavy_in_noisy)

    # Returns this probability
    return prob_heavy_in_noisy

You can test a single circuit below to see if it passes.

percent_heavy_sampled(parameters, permutations, 1, True)

The Median for this circuit is:
0.04363711
The heavy bitstrings for this circuit are
['0000', '0100', '0010', '1010', '0101', '1101', '0011', '0111']
This circuit has an ideal havy sampling probability of:
0.8153219893574715
Percent of time noisy sample returned heavy bitstring
0.488

0.488

The true quantum volume is detemined by repeating the process many times and averaging the results. This function repeatedly applies the percent _heavy_sampled function for n_circuitnumber of times and prints if the test is passed and returns the average.

def calc_qv(n_circuits, circuit_size, prob_of_error) -> float:

    n = circuit_size
    su4_per_circuit = int(n / 2 * n)
    number_of_circuits = n_circuits

    counter = 0
    circuit_results = []

    # Loop over n_circuits
    while counter < number_of_circuits:
        parameters = generate_random_params()
        permutations = generate_random_permutations()
        circuit_results.append(
            percent_heavy_sampled(parameters,
                                  permutations,
                                  prob_of_error,
                                  print_output=False))

        counter += 1

    # Average the results
    score = sum(circuit_results) / len(circuit_results)

    print('The score is:')
    print(score)

    # Determined if QV test is passed
    if score > 2 / 3:
        print('passed!')
        print('Quantum Volume')
        print(2**n)

    else:
        print('failed QV Test')

    return score

Try running the QV procedure for 100 four qubit circuits with a 10% chance of error

n = 4
calc_qv(100, n, .1)

The score is:
0.7280300000000003
passed!
Quantum Volume
16

0.7280300000000003

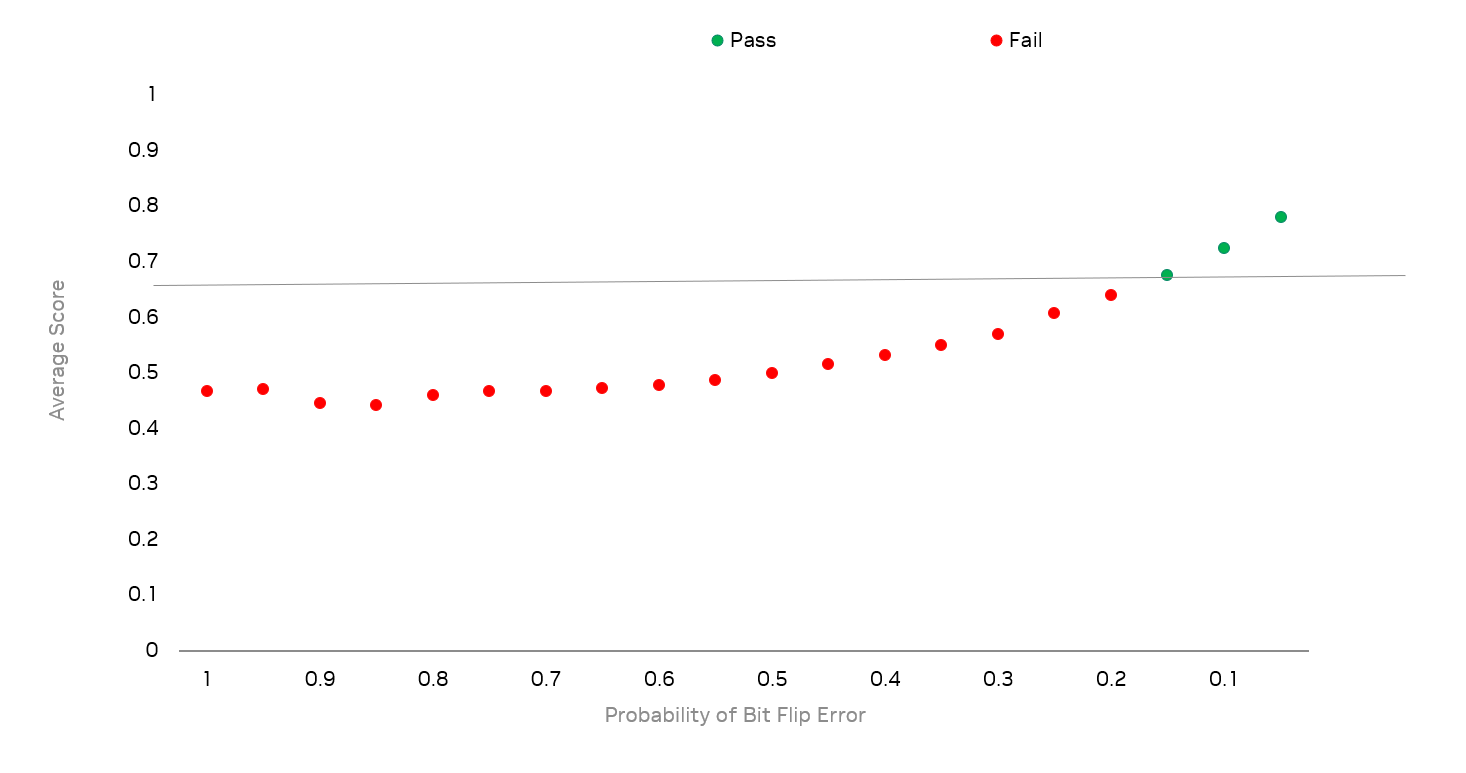
an interesting benefit of simulation is the ability to explore how noise might affect the QV results. In this case, the noise model is trivial, but it is still possible to see a relationship between the probability of error in the \(X\) gates and the QV outcome.