ADAPT-QAOA algorithm

In this tutorial, we explain the ADAPT-QAOA algorithm introduced in this paper and show how to implement the algorithm in cudaq.

In QAOA (explained in this Tutorial), the variational Ansatz consists of \(p\) layers, each containing the cost Hamiltonian \(H_C\) and a mixer, \(H_M\).

\[\ket{\psi_p (\beta, \gamma)} = \left ( \prod_{k=1} ^p [e^{-i H_M \beta_k} e^{-i H_C \gamma_k}] \right ) \ket{\psi_{\mathrm{ref}}}\]

where \(\ket{\psi_{\mathrm{ref}}} = \ket{+}^{\otimes n}\), \(n\) is the number of qubits and \(\gamma, \beta\) are set of variational parameters. If these parameters are chosen such that

\[\braket{\psi_p (\beta, \gamma)| H_C |\psi_p (\beta, \gamma) }\]

is minimized, then the resulting energy and state provide an approximate solution to the optimization problem encoded in \(H_C\). In the standard QAOA Ansatz, the mixer is chosen to be a single-qubit X rotation applied to all qubits.

In ADAPT-QAOA, the single, fixed mixer \(H_M\) is replaced by a set of mixers \(A_k\) that change from one layer to the next.

\[\ket{\psi_p (\beta, \gamma) } = \left ( \prod_{k=1} ^p [e^{-i A_k \beta_k} e^{-i H_C \gamma_k}] \right ) \ket{\psi_{\mathrm{ref}}}\]

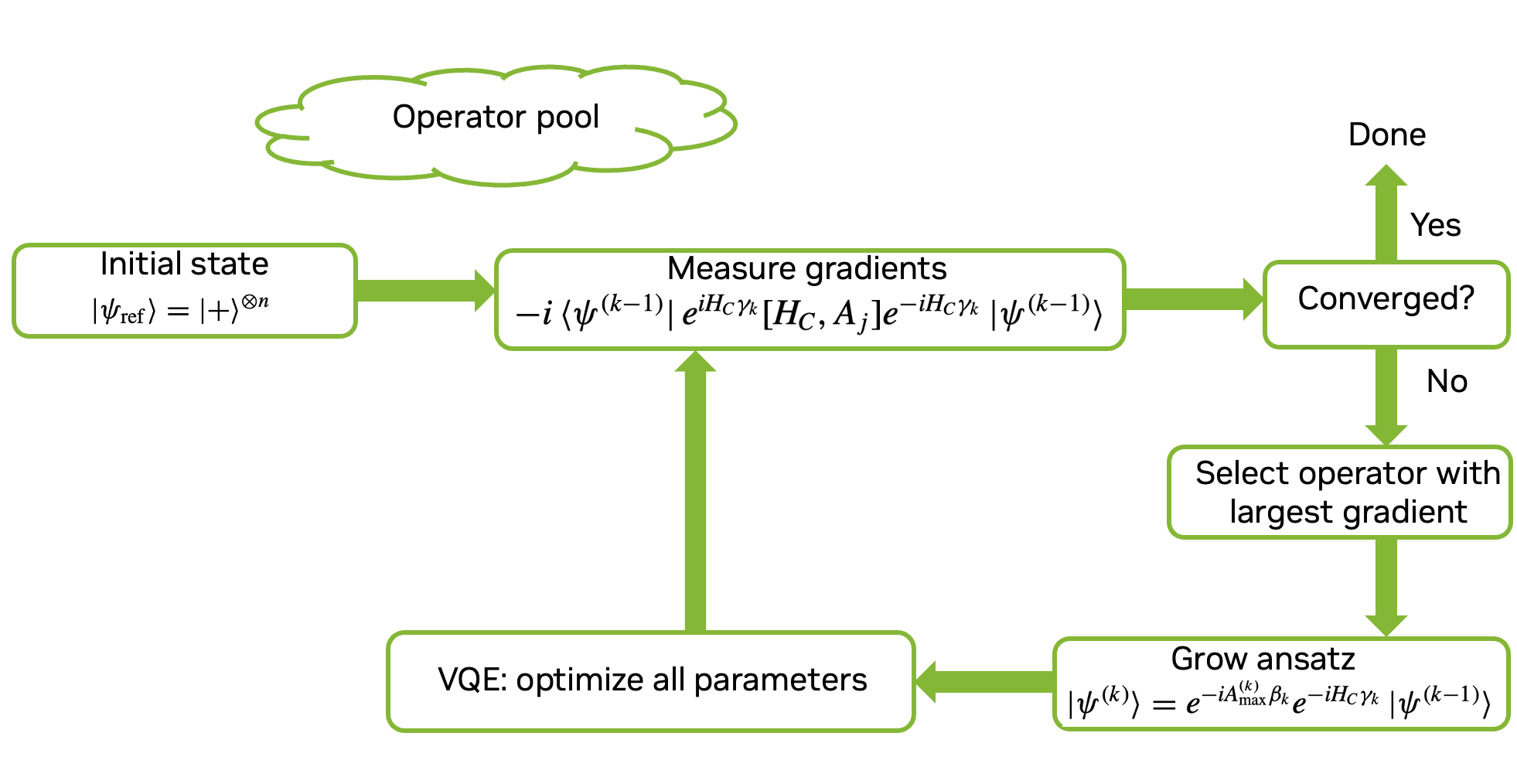
The ADAPT-QAOA algorithm can be summarized in three steps:

1- Define the operator set \(A_j\) (called the mixer pool, and where \(A_j = A^{\dagger}_j\) and select a suitable reference state to be the initial state: \(\ket{ \psi (0) }= \ket{\psi_{\mathrm{ref}}}\); \(\ket{\psi_{\mathrm{ref}}} = \ket{+}^{\otimes n}\) is chosen as in the standard QAOA

2- Prepare the current Ansatz \(\ket{\psi(k-1)}\) and measure the energy gradient with respect to the pool, the \(j\)th component of which is given by \(−i \braket{\psi(k-1)|e^{i H_C \gamma_k} [H_C,A_j] e^{−i H_C \gamma_k} |\psi(k-1)}\), where the new variational parameter \(\gamma_k\) is set to a predefined value \(\gamma_0\). For the measurement, we can decompose the commutator into linear combinations of Pauli strings and measure the expectation values of the strings using general variational quantum algorithm methods. If the norm of the gradient is below a predefined threshold, then the algorithm stops, and the current state and energy estimate approximate the desired solution. If the gradient threshold is not met, modify the Ansatz (k) by adding the operator, A(k) , associated with the largest max component of the gradient: \(\ket{\psi(k)}= e^ {−i A_\mathrm{max} \beta_k} e^{−i H_C \gamma_k} \ket{\psi(k-1)}\), where \(\beta_k\) is a new variational parameter

3- Optimize all parameters currently in the Ansatz \(\beta_m, \gamma_m = 1, 2, ...k\) such that \(\braket{\psi (k)|H_C|\psi(k)}\) is minimized, and return to the second step.

Below is a schematic representation of the ADAPT-QAOA algorithm explained above.

import numpy as np
import cudaq
from scipy.optimize import minimize
import random

cudaq.set_target("nvidia", option="fp64")

Simulation input:

The gradients used to select new operators are sensitive to the initial values for \(\gamma\). We initialize the parameter at \(\gamma_0 =0.01\) as explained in the paper.

# The Max-cut graph:

# Example 1
#true_energy=-12.0
#nodes = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
#edges = [[0,4], [1,4], [0,6], [3,6], [5,6], [2,7], [1,8], [3,8], [5,8], [6,8], [7,8], [2,9], [8,9]]
#weight = [1.0] * len(edges)

# Examle 2:
#true_energy=-5.0
nodes = [0, 1, 2, 3, 4]
edges = [[0, 1], [1, 2], [2, 3], [3, 0], [2, 4], [3, 4]]
weight = [1.0] * len(edges)

# Define the number of qubits.

qubits_num = len(nodes)

# Predefined values to terminate iteration. These can be changed based on user preference
E_prev = 0.0
threshold = 1e-3   # This is a predefined value to stop the calculation. if norm of the gradient smaller than this value, calculation will be terminated.
e_stop = 1e-7      # This is a predefined value to stop the calculation. if dE <= e_stop, calculation stop. dE=current_erg-prev_erg

# Initiate the parameters gamma of the problem Hamiltonian for gradient calculation

init_gamma = 0.01

The problem Hamiltonian \(H_C\) of the max-cut graph:

\[H_C= - \frac{1}{2} \sum_{i,j} \omega_{i,j} (I - Z_i Z_j)\]

def spin_ham (edges, weight):

    ham = 0

    count = 0
    for edge in range(len(edges)):

        qubitu = edges[edge][0]
        qubitv = edges[edge][1]
        # Add a term to the Hamiltonian for the edge (u,v)
        ham += 0.5 * (weight[count] * cudaq.spin.z(qubitu) * cudaq.spin.z(qubitv) -
                            weight[count] * cudaq.spin.i(qubitu) * cudaq.spin.i(qubitv))
        count += 1

    return ham

# Collect coefficients from a spin operator so we can pass them to a kernel
def term_coefficients(ham: cudaq.SpinOperator) -> list[complex]:
    result = []
    for term in ham:
        result.append(term.evaluate_coefficient())
    return result

# Collect Pauli words from a spin operator so we can pass them to a kernel
def term_words(ham: cudaq.SpinOperator) -> list[str]:
    # Our kernel uses these words to apply exp_pauli to the entire state.
    # we hence ensure that each pauli word covers the entire space.

    result = []
    for term in ham:
        result.append(term.get_pauli_word(qubits_num))
    return result

# Generate the Spin Hamiltonian:

ham = spin_ham(edges, weight)
ham_coef = term_coefficients(ham)
ham_word = term_words(ham)

Th operator pool \(A_j\):

Here, the mixer pool consists of qaoa mixer, single-qubit, and multi-qubit entangling gates. Note that more single and multi-qubit gates can be added based on the problem. Because of symmetry, we only includes the mixer pools that will have nonzero gradients as explained in the paper

def qaoa_mixer(n):

    term = cudaq.spin.x(0)

    for i in range(1, n):
        term = term + cudaq.spin.x(i)

    pool = [term]
    return pool

def qaoa_single_x(n):

    pool = []

    for i in range(n):
        pool.append(cudaq.spin.x(i))

    return pool

def qaoa_double_ops(n):

    pool = []

    for i in range(n-1):
        for j in range(i+1, n):
            pool.append(cudaq.spin.x(i) * cudaq.spin.x(j))
            pool.append(cudaq.spin.y(i) * cudaq.spin.y(j))
            pool.append(cudaq.spin.y(i) * cudaq.spin.z(j))
            pool.append(cudaq.spin.z(i) * cudaq.spin.y(j))

    return pool

def mixer_pool(qubits_num):
    return (
          qaoa_single_x(qubits_num)
        + qaoa_mixer(qubits_num)
        + qaoa_double_ops(qubits_num)
    )

# Generate the mixer pool

pools = mixer_pool(qubits_num)
print('Number of pool operator: ', len(pools))

Number of pool operator:  46

The commutator \([H_C,A_j]\):

# Generate the commutator [H,Ai]

def commutator(pools, ham):
    com_op = []

    for i in range(len(pools)):
    #for i in range(2):
        op = pools[i]
        com_op.append(ham * op - op * ham)

    return com_op

grad_op = commutator(pools, ham)

###########################################
# Get the initial state (psi_ref)

@cudaq.kernel
def initial_state(qubits_num:int):
    qubits = cudaq.qvector(qubits_num)
    h(qubits)

state = cudaq.get_state(initial_state, qubits_num)

#print(state)
###############################################

# Circuit to compute the energy gradient with respect to the pool
@cudaq.kernel
def grad(state:cudaq.State, ham_word:list[cudaq.pauli_word], ham_coef: list[complex], init_gamma:float):
    q = cudaq.qvector(state)

    for i in range(len(ham_coef)):
        exp_pauli(init_gamma * ham_coef[i].real, q, ham_word[i])


# The qaoa circuit using the selected pool operator with max gradient

@cudaq.kernel
def kernel_qaoa(qubits_num:int, ham_word:list[cudaq.pauli_word], ham_coef:list[complex],
        mixer_pool:list[cudaq.pauli_word], gamma:list[float], beta:list[float], layer:list[int], num_layer:int):

    qubits = cudaq.qvector(qubits_num)

    h(qubits)

    idx = 0
    for p in range(num_layer):
        for i in range(len(ham_coef)):
            exp_pauli(gamma[p] * ham_coef[i].real, qubits, ham_word[i])

        for j in range(layer[p]):
            exp_pauli(beta[idx+j], qubits, mixer_pool[idx+j])
        idx = idx + layer[p]

Beginning of ADAPT-QAOA iteration:

Note that, here in this tutorial, we set the seed for the random number generator. This ensures that the random choices are reproducible in each step of iteration when choosing operator pools if more than one operator pool has the same value. For production, users need to change that.

# Begining od ADAPT-QAOA iteration

beta = []
gamma = []

mixer_pool = []
layer = []


istep = 1
while True:

    print('Step: ', istep)

    #####################
    # compute the gradient and find the mixer pool with large values.
    # If norm is below the predefined threshold, stop calculation

    gradient_vec = []
    for op in grad_op:
        op = op * -1j
        gradient_vec.append(cudaq.observe(grad, op , state, ham_word, ham_coef, init_gamma).expectation())

    # Compute the norm of the gradient vector
    norm = np.linalg.norm(np.array(gradient_vec))
    print('Norm of the gradient: ', norm)

    if norm <= threshold:
        print('\n', 'Final Result: ', '\n')
        print('Final mixer_pool: ', mixer_pool)
        print('Number of layers: ', len(layer))
        print('Number of mixer pool in each layer: ', layer)
        print('Final Energy: ', result_vqe.fun)

        break

    else:
        temp_pool = []
        tot_pool = 0

        max_grad = np.max(np.abs(gradient_vec))

        for i in range(len(pools)):
            if np.abs(gradient_vec[i]) >= max_grad:
                tot_pool += 1
                temp_pool.append(pools[i])

        # Set the seed for the random number generator
        # This ensures that the random choices are reproducible
        # in each step of the iteration.
        random.seed(42)

        layer.append(1)
        random_mixer = random.choice(temp_pool)

        mixer_pool = mixer_pool + [random_mixer.get_pauli_word(qubits_num)]

        print('Mixer pool at step', istep)
        print(mixer_pool)

        num_layer = len(layer)
        print('Number of layers: ', num_layer)

        beta_count = layer[num_layer-1]
        init_beta = [0.0] * beta_count
        beta = beta + init_beta
        gamma = gamma + [init_gamma]
        theta = gamma + beta

        def cost(theta):

            theta = theta.tolist()
            gamma = theta[:num_layer]
            beta = theta[num_layer:]


            energy = cudaq.observe(kernel_qaoa, ham, qubits_num, ham_word, ham_coef,
                                    mixer_pool, gamma, beta, layer, num_layer).expectation()
            #print(energy)
            return energy

        result_vqe = minimize(cost, theta, method='BFGS', jac='2-point', tol=1e-5)
        print('Result from the step ', istep)
        print('Optmized Energy: ', result_vqe.fun)

        dE = np.abs(result_vqe.fun - E_prev)
        E_prev = result_vqe.fun
        theta = result_vqe.x.tolist()
        erg = result_vqe.fun

        print('dE= :', dE)
        gamma=theta[:num_layer]
        beta=theta[num_layer:]

        if dE <= e_stop:
            print('\n', 'Final Result: ', '\n')
            print('Final mixer_pool: ', mixer_pool)
            print('Number of layers: ', len(layer))
            print('Number of mixer pool in each layer: ', layer)
            print('Final Energy= ', erg)

            break

        else:

            # Compute the state of this current step for the gradient
            state = cudaq.get_state(kernel_qaoa, qubits_num, ham_word, ham_coef,mixer_pool, gamma, beta, layer, num_layer)
            #print('State at step ', istep)
            #print(state)
            istep+=1
            print('\n')

Step:  1
Norm of the gradient:  3.468398683655509
Mixer pool at step 1
['IIZIY']
Number of layers:  1
Result from the step  1
Optmized Energy:  -3.4999999999998064
dE= : 3.4999999999998064


Step:  2
Norm of the gradient:  2.4501630553527365
Mixer pool at step 2
['IIZIY', 'ZIIYI']
Number of layers:  2
Result from the step  2
Optmized Energy:  -3.999999999998128
dE= : 0.4999999999983218


Step:  3
Norm of the gradient:  1.99990001175888
Mixer pool at step 3
['IIZIY', 'ZIIYI', 'ZYIII']
Number of layers:  3
Result from the step  3
Optmized Energy:  -4.499999999929474
dE= : 0.49999999993134603


Step:  4
Norm of the gradient:  0.014141961855183087
Mixer pool at step 4
['IIZIY', 'ZIIYI', 'ZYIII', 'IIXIX']
Number of layers:  4
Result from the step  4
Optmized Energy:  -4.999999999996581
dE= : 0.5000000000671072


Step:  5
Norm of the gradient:  5.778820729079865e-06

 Final Result:

Final mixer_pool:  ['IIZIY', 'ZIIYI', 'ZYIII', 'IIXIX']
Number of layers:  4
Number of mixer pool in each layer:  [1, 1, 1, 1]
Final Energy:  -4.999999999996581

print('\n', 'Sampling the Final ADAPT QAOA circuit', '\n')
# Sample the circuit
count=cudaq.sample(kernel_qaoa, qubits_num, ham_word, ham_coef,mixer_pool, gamma, beta, layer, num_layer, shots_count=5000)
print('The most probable max cut: ', count.most_probable())
print('All bitstring from circuit sampling: ', count)

 Sampling the Final ADAPT QAOA circuit

The most probable max cut:  01011
All bitstring from circuit sampling:  { 01011:2550 10100:2450 }

print(cudaq.__version__)

CUDA-Q Version cu12-latest (https://github.com/NVIDIA/cuda-quantum 05873efb8973bd60fcf7cfe193e6ab54c6edee60)