Quantum Teleporation

Below we shall study an interesting quantum phenomena - teleportation.

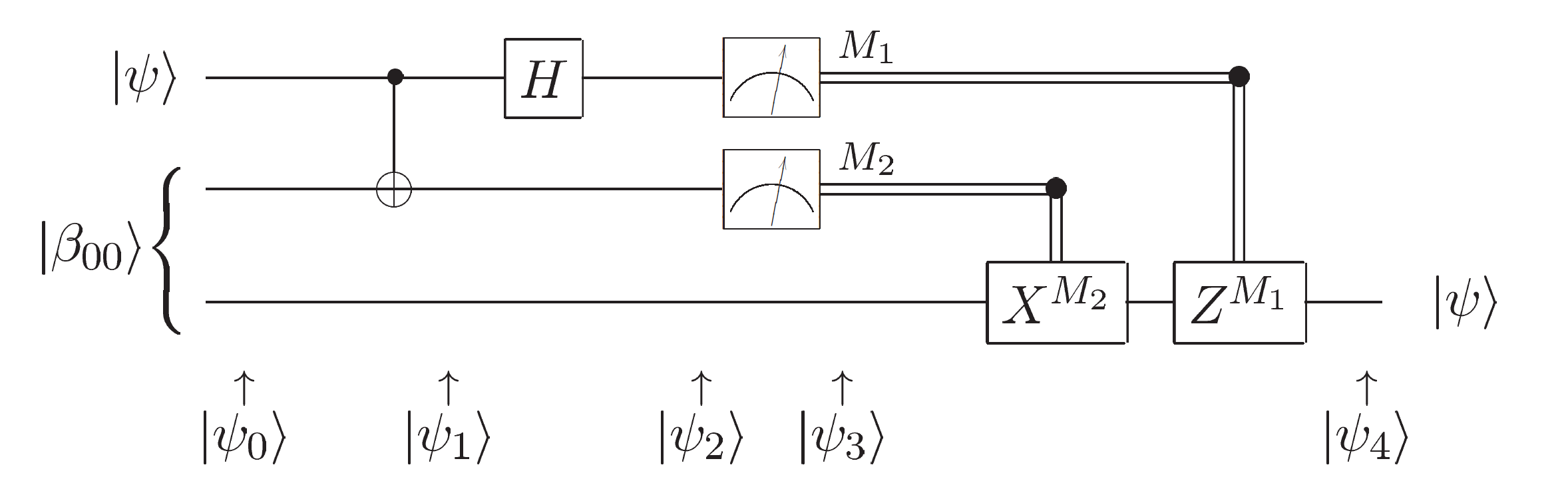
Let us start by implementing the circuit shown below and discuss its implications later. We normally assume that the input qubits are initialised to the \(\ket{0}\) state unless specified otherwise. In this case however, the circuit diagram depicts the 0th qubit to be initialised in an arbitary quantum state, \(\ket{\psi} = \alpha\ket{0} + \beta\ket{1}\), and the 1st and 2nd qubit to be in the state \(\ket{\beta_{00}} = \tfrac{1}{\sqrt{2}} [\ket{00} + \ket{11}]\).

import cudaq
import numpy as np

cudaq.set_target('qpp-cpu')
cudaq.set_random_seed(23)

# We now replicate the circuit shown in the diagram above and step through each intermediate stage from psi0 to psi4.


@cudaq.kernel
def teleportation():

    # Initialize a 3 qubit quantum circuit
    qubits = cudaq.qvector(3)

    # Psi0 - random quantum state, psi, on qubit 0.
    rx(3.14, qubits[0])
    ry(2.71, qubits[0])
    rz(6.62, qubits[0])

    # Psi0 - create a maximally entangled state on qubits 1 and 2.
    h(qubits[1])
    cx(qubits[1], qubits[2])


# Let us save the statevector of the circuit so far for later use.
psi_0 = cudaq.get_state(teleportation)

# Now we continue with the rest of the circuit


@cudaq.kernel
def teleportation():

    # Initialize a 3 qubit quantum circuit
    qubits = cudaq.qvector(3)

    # Psi0 - random quantum state, psi, on qubit 0.
    rx(3.14, qubits[0])
    ry(2.71, qubits[0])
    rz(6.62, qubits[0])

    # Psi0 - create a maximally entangled state on qubits 1 and 2.
    h(qubits[1])
    cx(qubits[1], qubits[2])

    # Psi1
    cx(qubits[0], qubits[1])

    # Psi2
    h(qubits[0])

    # Psi3 - measure qubits 0 and 1 and store it in variables m1 and m2
    m1 = mz(qubits[0])
    m2 = mz(qubits[1])

    # Psi4 - apply conditioned pauli operators dependent on the measurement result of qubits 0 and 1.
    if m1 == 1:
        z(qubits[2])

    if m2 == 1:
        x(qubits[2])


psi_4 = cudaq.get_state(teleportation)

The state of this 3 qubit system is described by a \(2^3 = 8\) dimensional vector. Sometimes we would like to extract the state of a single qubit from a multipartite state. We can use the partial trace operation defined in the function below which allows us to translate our statevectors to the density matrix representation to trace out subsystems.

# Function to be used below to calculate the partial trace yielding a density matrix.


def partial_trace(state_vector, trace_systems):
    """
    Partial trace of multi-particle quantum state.

    Arguments:
        state_vector: complex vector  of size 2**n
        trace_systems (list(int)): a list of subsystems (starting from 0) to trace over.
        dimensions (list(int)): a list of the dimensions of the subsystems.

    Returns:
        ndarray: A density matrix with the appropriate subsystems traced over.
    """

    n_qubits = int(np.log2(state_vector.shape[0]))

    dimensions = [2 for i in range(n_qubits)]

    trace_systems = len(dimensions) - 1 - np.array(trace_systems)

    rho = state_vector.reshape(dimensions)
    rho = np.tensordot(rho, rho.conj(), axes=(trace_systems, trace_systems))
    d = int(np.sqrt(np.prod(rho.shape)))

    return rho.reshape(d, d)

# Trace out qubits 1 and 2 leaving us with qubit 0.
state_of_q0 = partial_trace(state_vector=np.array(psi_0), trace_systems=[1, 2])

# Trace out qubits 0 and 1 leaving us with qubit 2.
state_of_q2 = partial_trace(state_vector=np.array(psi_4), trace_systems=[0, 1])

print(f"|qubit_0> == |qubit_2>?  {np.allclose(state_of_q0, state_of_q2)}")

|qubit_0> == |qubit_2>?  True

Let us discuss what has happened.

We started with a 3 qubit quantum circuit with the 0th qubit in \(\ket{\psi}\) and the 2nd qubit being a portion of the maximally entangled bell state \(\ket{\beta_{00}}\).

If we look closely at the code cell above, the output state on the 2nd qubit, state_of_q2, is the same as the random input state, \(\ket{\psi}\), on the 0th qubit, state_of_q0.

We have teleported a quantum state from one qubit to another. There is nothing to restrict how close qubits 0 and 2 have to be since they have no entangling operations between them. They can be placed in different labs or infinitely far apart.

Moreover, we still obey the no-cloning theorem since the initial state \(\ket{\psi}\) no longer exists on the 0th qubit and hence we only have 1 copy of it as shown below

# Using the final statevector, psi4, we show that psi has been teleported and only 1 copy of psi is preserved.

# Trace out qubits 1 and 2 leaving us with qubit 0
state_of_q0 = partial_trace(state_vector=np.array(psi_4), trace_systems=[1, 2])

# Trace out qubits 0 and 1 leaving us with qubit 2
state_of_q2 = partial_trace(state_vector=np.array(psi_4), trace_systems=[0, 1])

np.allclose(state_of_q0, state_of_q2)

False

None of this violates the universal limit of information travelling faster than the speed of light. Notice how we have conditioned operations meaning we have to communicate classical information via classical channels which adhere to this limit.

Teleportation explained

We have stepped through the circuit above using code. We will now do the same using mathematics to enhance our understanding.

We start by gathering experimentalists in a lab and performing the following

\[\begin{split}\begin{aligned} CX_{01}H_{0}\ket{00} &= CX_{01}\tfrac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{0} \\ &= CX_{01}\tfrac{1}{\sqrt{2}}(\ket{00}+\ket{10}) \\ &= \tfrac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \\ &= \ket{\beta_{00}} \end{aligned}\end{split}\]

to create an entangled bell pair. We then hand each qubit in \(\ket{\beta_{00}}\) to two parties, namely Alice and Bob for safekeeping. Many moons later, Alice comes in posession of an arbitary quantum state \(\ket{\psi} = \alpha\ket{0} + \beta\ket{1}\) which she would like to send to Bob who is many miles away. This entails communicating values of \(\alpha\) and \(\beta\). However, measurement would lead to state collapse and only yield one bit of information, 0 or a 1.

Referring to circuit in the figure above, the 0th and the 1st qubits are in posession of Alice and the 2nd qubit is with Bob. The 1st and 2nd qubits have been entangled but are now seperated in distance. Let us now step through the circuit to describe its evolution. Our input state is

\[\begin{split}\begin{aligned} \ket{\psi_{0}} &= \ket{\psi} \ket{\beta_{00}} = (\alpha\ket{0} + \beta\ket{1})(\tfrac{1}{\sqrt{2}} (\ket{00} + \ket{11}) \\ &= \tfrac{1}{\sqrt{2}}[\alpha\ket{0}(\ket{00} + \ket{11}) +\beta\ket{1}(\ket{00} + \ket{11})] \end{aligned}\end{split}\]

Alice then performs a CX gate between the qubits she posses i.e. qubit 0 and 1

\[\begin{split}\begin{aligned} \ket{\psi_{1}} &= CX_{01}\ket{\psi_{0}} \\ &= \tfrac{1}{\sqrt{2}}[\alpha\ket{0}(\ket{00} + \ket{11}) +\beta\ket{1}(\ket{10} + \ket{01})] \end{aligned}\end{split}\]

which is then followed by Alice performing a Hadamard on the 0th qubit

\[\begin{split}\begin{aligned} \ket{\psi_{2}} &= H_{0}\ket{\psi_{1}} \\ &= \tfrac{1}{{2}}[\alpha(\ket{0}+\ket{1})(\ket{00} + \ket{11}) +\beta(\ket{0}-\ket{1})(\ket{10} + \ket{01})]. \end{aligned}\end{split}\]

If we expand all the inner brackets

\[\begin{split}\begin{aligned} \ket{\psi_{2}} &= \tfrac{1}{{2}}[(\alpha\ket{0} + \alpha\ket{1})(\ket{00} + \ket{11}) + (\beta\ket{0} - \beta\ket{1})(\ket{10} + \ket{01})] \\ &= \tfrac{1}{{2}}[\alpha\ket{000}+\alpha\ket{011} +\alpha\ket{100} +\alpha\ket{111} +\beta\ket{010}+\beta\ket{001}-\beta\ket{110}-\beta\ket{101}] \end{aligned}\end{split}\]

and then collect like terms whilst maintaining qubit ordering, we yield

\[\begin{aligned} \ket{\psi_{2}} &= \tfrac{1}{{2}}[ \ket{00}(\alpha\ket{0}+\beta\ket{1}) + \ket{01}(\alpha\ket{1}+\beta\ket{0}) + \ket{10}(\alpha\ket{0}-\beta\ket{1}) + \ket{11}(\alpha\ket{1}+\beta\ket{0}) ] \end{aligned}\]

where the qubit ordering notation states that the left most qubit is the 0th qubit. This expression naturally breaks down into 4 terms where each term has all 3 qubits and the 4 terms represent all the possibilities they can be in after they have been evolved.

We now ask our friend Alice to measure her qubits. Quantum mechanically we know that upon measurement the possibilities of the 3 qubit system will collapse regardless of the distance between them and the unmeasured outcomes will therefore be deterministic. If her measurement result yields a 00, the first term in \(\ket{\psi_{2}}\) tells us that Bob’s qubit will be in the state \(\alpha\ket{0}+\beta\ket{1}\) which is the the original state, \(\ket{\psi}\), we wanted to teleport. Alice has other potential measurement outcomes all of which are summarised in the figure below

Alices’ measurement	Bobs’ state
\[00\]	\[\ket{\psi_3(00)} = \alpha\ket{0} + \beta\ket{1}\]
\[01\]	\[\ket{\psi_3(01)} = \alpha\ket{1} + \beta\ket{0}\]
\[10\]	\[\ket{\psi_3(10)} = \alpha\ket{0} - \beta\ket{1}\]
\[11\]	\[\ket{\psi_3(11)} = \alpha\ket{1} - \beta\ket{0}\]

A quick glance at the figure above shows us that Bob’s qubit is nearly in the state \(\ket{\psi}\) which is what we are after pending some minor corrections. The circuit diagram depicts conditioned gates that are applied depending on Alice’s measurement result fulfilling the minor corrections required to complete the teleportation protocol. The final gate operations are summarised below

\[\begin{split}\begin{aligned} M1M2 = 00, \ket{\psi_4} = Z^{0}X^{0}\ket{\psi_3(00)} = \alpha\ket{0} + \beta\ket{1} = \ket{\psi} \\ M1M2 = 01, \ket{\psi_4} = Z^{0}X^{1}\ket{\psi_3(01)} = \alpha\ket{0} + \beta\ket{1} = \ket{\psi} \\ M1M2 = 10, \ket{\psi_4} = Z^{1}X^{0}\ket{\psi_3(10)} = \alpha\ket{0} + \beta\ket{1} = \ket{\psi} \\ M1M2 = 11, \ket{\psi_4} = Z^{1}X^{1}\ket{\psi_3(11)} = \alpha\ket{0} + \beta\ket{1} = \ket{\psi} \end{aligned}\end{split}\]

It is clear to see that in all instances, we recover \(\ket{\psi}\) on Bob’s qubit thus fulfilling our ambition of teleporting an unknown quantum state between 2 parties.

It is important to note that quantum teleportation does not allow communication faster than the speed of light. The state \(\ket{\psi}\) does not instantly appear with Bob. Alice has to use a classical communication channel which is bound by the speed of classical physics to communicate her measurement results to Bob so that he can make the minor corrections required.

Moreover teleportation does not violate the no-cloning theorem. The protocol does not allow us to create a copy of \(\ket{\psi}\) leaving us with \(\ket{\psi\psi}\) but rather transmits \(\ket{\psi}\) from Alice to Bob.

The images used in this notebook are courtesey of the Quantum Computation and Quantum Information textbook by Nielsen & Chuang.