Factoring Integers With Shor’s Algorithm¶
The most famous application of quantum computers is factoring integers using Shor’s algorithm. This algorithm is particularly significant because an efficient factorization algorithm could potentially break modern asymmetric encryption schemes, such as RSA.
For small integers, this quantum algorithm can be simulated on classical computers. The main challenge in classical implementation lies in the order-finding algorithm. We will first introduce the classical implementation of this algorithm as a preliminary step, and then proceed to explain the quantum order-finding algorithm.
First let’s install some libraries.
[ ]:
!pip install contfrac==1.0.0 -q
[156]:
from math import gcd, log2, ceil
import numpy as np
import random
import cudaq
from cudaq import *
import fractions
import matplotlib.pyplot as plt
import contfrac
Shor’s algorithm¶
The factoring problem for an integer \(N\) aims to find integers \(a_1\), \(a_2\) which are factors of \(N\). This problem is interesting when \(N\) is not prime and the solutions \(a_1\) and \(a_2\) are non-trivial. In other words, we will attempt to find integers \(a_1\) and \(a_2\) satisfying \(N=a_1\cdot a_2\) with \(a_1\neq 1\) and \(a_2\neq 1\).
The algorithm consists of two ideas:
Reduce the problem of factoring the integer \(N\) to the order-finding problem.
Solve the order-finding problem: Given integers \(a\) and \(N\) so that \(a\) and \(N\) share no common factors (i.e., the greatest common divisor of \(a\) and \(N\) is 1), find the smallest positive integer which satisfies \(a^r \equiv 1 \mod N\). This value \(r\) is refered to as the order of \(a \mod N\).
These two ideas are combined in the following steps in Shor’s algorithm:
Rule out the easy case that \(N\) is even
Select a random integer \(a\) between \(2\) and \(N-1\)
Check to see if \(a\) is a factor of \(N\) (if so we’re done!)
Find the order of \(a \mod N\), (i.e., find \(r\) so that \(a^r\equiv 1 \mod N\))
Check to see if \(a^{\frac{r}{2}}-1\) or \(a^{\frac{r}{2}}+1\) are integers and share common, non-trivial, divisors with \(N\) (if so we’re done!)
If no factor is found, repeat steps 1 through 4 above.
The function shors_algorithm below outlines these steps for both the classical and the quantum implementation of Shor’s algorithm. For the purposes of demonstration, we will also control the initial random integer selected in step 1 so that we can investigate cases in which the selected integer produces common divisors of \(N\) in step 4 and others in which step 4 produces no common factors.
Note about terminology: Some literature refers to the “period-finding problem” in Shor’s algorithm. The order-finding problem, as we have described above, can be recast as finding the period of the function \(f(x) = a^x\mod N\), by noticing that the period of \(f(x)\) is one more than the order of \(a\mod N\). The period finding problem is more general than the order-finding problem since it aims to find the period of any periodic function, not just modular exponentiation.
[3]:
def shors_algorithm(N, initial, quantum):
""" Factor N using Shor's algorithm with initial starting value and choice of
using either classical or quantum approach for the period finding step
Parameters
----------
N: int
Integer to be factored (assumed to be non-prime and >1)
initial: int
Initial choice of the random integer between 2 and N-1
quantum: boolean
True if we will call the quantum order-finding algorithm, and false if we call the classical one for step 3.
Returns
-------
a1, a2: int
Non-trivial factors of N
"""
# 0. Check to see if N is even.
if N % 2 == 0:
divisor1 = 2
divisor2 = N // 2
print("Found factors:", divisor1, divisor2)
return (divisor1, divisor2)
attempts = [initial]
while (True):
# 1. Select a random integer between 2 and N-1
if len(attempts) == 1:
a = initial
else:
a = random.choice(
[n for n in range(N - 1) if n not in attempts and n != 1])
# 2. See if the integer selected in step 1 happens to factor N
print("Trying a =", a)
divisor1 = gcd(a, N)
if divisor1 != 1:
divisor2 = N // divisor1
print("Found factors of N={} by chance: {} and {}".format(
N, divisor1, divisor2))
return (divisor1, divisor2)
# 3. Find the order of a mod N (i.e., r, where a^r = 1 (mod N))
if quantum == True:
r = find_order_quantum(a, N)
else:
r = find_order_classical(a, N)
print("The order of a = {} is {}".format(a, r))
# 4. If the order of a is found and it is
# * even and
# * not a^(r/2) = -1 (mod N),
# then test a^(r/2)-1 and a^(r/2)+1 to see if they share factors with N.
# We also want to rule out the case of finding the trivial factors: 1 and N.
divisor1, divisor2 = test_order(a, r, N)
if (divisor1 != 0): # test_order will return a 0 if no factor is found
print("Found factors of N = {}: {} and {}".format(
N, divisor1, divisor2))
return divisor1, divisor2
# 5. Repeat
print("retrying...")
attempts.append(a)
Let’s first explore the idea of reducing the factoring problem into the order-finding problem. This gets captured in step 4 described above. In this step, we have already established that \(a\) and \(N\) share no factors other than \(1\) (i.e., \(\gcd(a,N)=1\)) and we have found \(r\), the order of \(a\mod N.\) With this information we know that \(a^r \equiv 1 \mod N.\) Rewritten in another way:
If \(r\) is even, we can rewrite \(a^r\) as \(x^2\) where \(x=a^\frac{r}{2}\). Next, we can factor equation \((1)\) using the identity \(x^2-1 = (x-1)(x+1)\):
If, in addition, the equation
is satisfied, then at least one of the terms \(a^{\frac{r}{2}} - 1\) or \(a^{\frac{r}{2}} + 1\) must share a common factor with \(N\). Peter Shor demonstrated that there is greater than a \(50\%\) chance of randomly selecting a value for \(a\) satisfying these properties.
The code block below defines a function that tests whether \(r\) is even and whether equation \((3)\) is satisfied and searches for a non-trivial factor of \(N\).
[157]:
def test_order(a, r, N):
"""Checks whether or not a^(r/2)+1 or a^(r/2)-1 share a non-trivial common factor with N
Parameters
----------
a: int
r: int
N: int
Returns
-------
int, int factors of N, if found; 0,0 otherwise
"""
if r != None and (r % 2 == 0) and a**r % N == 1:
if (a**(int(r / 2))) % N != -1:
possible_factors = [gcd(r - 1, N), gcd(r + 1, N)]
for test_factor in possible_factors:
if test_factor != 1 and test_factor != N:
return test_factor, N // test_factor
# period did not produce a factor
else:
print('No non-trivial factor found')
return 0, 0
Solving the order-finding problem classically¶
The key component of Shor’s algorithm is an efficient quantum algorithm to find the order \(r\) of \(a \mod N\). While a straightforward classical algorithm can solve this problem, it is notably inefficient:
[158]:
def find_order_classical(a, N):
"""A naive classical method to find the order r of a (mod N).
Parameters
----------
a: int
an integer in the interval [2,N-1]
N: int
Returns
-------
r: int
Period of a^x (mod N)
"""
assert 1 < a and a < N
r = 1
y = a
while y != 1:
y = y * a % N
r += 1
return r
Let’s see how Shor’s algorithm works on a few examples using the classical order-finding problem. Notice how often our choice of value for the initial guess for \(a\) produces factors of \(N\).
[159]:
my_integer = 123 #edit this value to try out a few examples
# Edit the value in the line below to try out different initial guesses for a.
# What happens when you choose a = 42 for the integer 123?
# What happens when you choose a = 100 for the integer 123?
initial_value_to_start = 42 # edit this value; it should be less than my_integer
shors_algorithm(my_integer, initial_value_to_start, False)
Trying a = 42
Found factors of N=123 by chance: 3 and 41
[159]:
(3, 41)
Solving the order-finding problem with a quantum algorithm¶
The Fourier transform is a classical computation that provides a more efficient algorithm than the one encoded in find_order_classical for identifying the period of \(f(x) = a^x\mod N\). The quantum version of the Fourier transform is the central idea of Shor’s Algorithm. This efficient quantum solution derives the period from a measurement of \(n = \lceil log2(N) \rceil\) qubits.
The image below outlines the quantum kernel used to find the order of \(a\). Notice the last step involves applying the Inverse Quantum Fourier Transform.
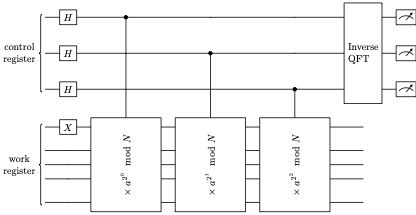
Figure. Circuit diagram for finding the phase of the modular multiplication gate \(U|x\rangle = |a^x\mod N\rangle\), which will be used to compute the order of \(a\) modulo \(N\). The number of qubits in the control register determines the accuracy of estimating the phase of \(U\). The size of the work register depends on \(N\). The goal of this section is to code the diagram as a kernel named phase_kernel.
We will need to create a quantum kernel for the Inverse Quantum Fourier Transform. Additionally we’ll need to create a kernel for modular multiplication: \(g(y) = ay \mod N\), which can be repeatedly applied \(x\)-times to \(y=1\) to carry our modular exponentation \(f(x)=a^x\mod N\).
Inverse quantum Fourier transform¶
In the code block below we define a kernel for the quantum Fourier transform and then use cudaq.adjoint to create a kernel for the inverse quantum Fourier transform used in the quantum order-finding algorithm.
[160]:
# Define kernels for the quantum Fourier transform and the inverse quantum Fourier transform
@cudaq.kernel
def quantum_fourier_transform(qubits: cudaq.qview):
qubit_count = len(qubits)
# Apply Hadamard gates and controlled rotation gates.
for i in range(qubit_count):
h(qubits[i])
for j in range(i + 1, qubit_count):
angle = (2 * np.pi) / (2**(j - i + 1))
cr1(angle, [qubits[j]], qubits[i])
@cudaq.kernel
def inverse_qft(qubits: cudaq.qview):
cudaq.adjoint(quantum_fourier_transform, qubits)
Quantum kernels for modular exponentiation¶
While Shor’s algorithm provably can factor numbers faster than known classical techniques, the resources required for implementing Shor’s algorithm are hefty. A full-scale implementation to factor an \(L\)-bit number could require a quantum kernel with \(5L+1\) qubits to achieve accuracy for the continued fractions part of the algoirthm and as many as \(72L^3\) quantum gates for the modular exponentiaion (Beckman, Chari, Devabhaktuni, & Preskill, 1996). Both of these are well beyond the capabilities of modern quantum hardware for numbers of interest. Advancements to reduce the number of gates and qubits required focus on optimizing the kernel for \(f(x) = a\cdot x \mod N\) for properties of the number to be factored. The difficulty is to create efficient quantum kernels (in terms of qubit and gate count) that compute \(a\cdot x \mod{N}\).
For the purposes of this demonstration, we will consider only the order-finding problem for the values of \(a\) to be either \(4\) or \(5\) with \(N=21\). We’ll be using the quantum circuits depicted in this paper and this report, respectively.
The case N = 21 and a = 5:¶
[161]:
@cudaq.kernel
def modular_mult_5_21(work: cudaq.qview):
""""Kernel for multiplying by 5 mod 21
based off of the circuit diagram in
https://physlab.org/wp-content/uploads/2023/05/Shor_s_Algorithm_23100113_Fin.pdf
Modifications were made to change the ordering of the qubits"""
x(work[0])
x(work[2])
x(work[4])
swap(work[0], work[4])
swap(work[0], work[2])
@cudaq.kernel
def modular_exp_5_21(exponent: cudaq.qview, work: cudaq.qview,
control_size: int):
""" Controlled modular exponentiation kernel used in Shor's algorithm
|x> U^x |y> = |x> |(5^x)y mod 21>
"""
x(work[0])
for exp in range(control_size):
ctrl_qubit = exponent[exp]
for _ in range(2**(exp)):
cudaq.control(modular_mult_5_21, ctrl_qubit, work)
Verify in the code block below that the kernels defined above do in fact carry out multiplication and exponentiation with \(a=5\) and \(N=21\) by changing the iterations variable below.
[198]:
# Demonstrate iterated application of 5y mod 21 where y = 1
@cudaq.kernel
def demonstrate_mod_exponentiation(iterations: int):
qubits = cudaq.qvector(5)
x(qubits[0]
) # initalizes the qubits in the state for y = 1 which is |10000>
for _ in range(iterations):
modular_mult_5_21(qubits)
shots = 200
# The iterations variable determines the exponent in 5^x mod 21.
# Change this value to verify that the demonstrate_mod_exponentiation
# kernel carries out the desired calculation.
iterations = 1
print(cudaq.draw(demonstrate_mod_exponentiation, iterations))
results = cudaq.sample(demonstrate_mod_exponentiation,
iterations,
shots_count=shots)
print("Measurement results from sampling:", results)
# Reverse the order of the most probable measured bit string
# and convert the binary string to an integer
integer_result = int(results.most_probable()[::-1], 2)
print("For x = {}, 5^x mod 21 = {}".format(iterations, (5**iterations) % 21))
print("For x = {}, the computed result of the circuit is {}".format(
iterations, integer_result))
╭───╮╭───╮
q0 : ┤ x ├┤ x ├─╳──╳─
╰───╯╰───╯ │ │
q1 : ───────────┼──┼─
╭───╮ │ │
q2 : ┤ x ├──────┼──╳─
╰───╯ │
q3 : ───────────┼────
╭───╮ │
q4 : ┤ x ├──────╳────
╰───╯
Measurement results from sampling: { 10100:200 }
For x = 1, 5^x mod 21 = 5
For x = 1, the computed result of the circuit is 5
The case N = 21 and a = 4:¶
The example below is one where the work register has been optimized to use fewer gates and qubits than would have been necessary through a straightforward implementation of modular multiplication as seen in the previous case.
[199]:
@cudaq.kernel
def modular_exp_4_21(exponent: cudaq.qview, work: cudaq.qview):
""" Controlled modular exponentiation kernel used in Shor's algorithm
|x> U^x |y> = |x> |(4^x)y mod 21>
based off of the circuit diagram in https://arxiv.org/abs/2103.13855
Modifications were made to account for qubit ordering differences"""
swap(exponent[0], exponent[2])
# x = 1
x.ctrl(exponent[2], work[1])
# x = 2
x.ctrl(exponent[1], work[1])
x.ctrl(work[1], work[0])
x.ctrl([exponent[1], work[0]], work[1])
x.ctrl(work[1], work[0])
# x = 4
x(work[1])
x.ctrl([exponent[0], work[1]], work[0])
x(work[1])
x.ctrl(work[1], work[0])
x.ctrl([exponent[0], work[0]], work[1])
x.ctrl(work[1], work[0])
swap(exponent[0], exponent[2])
Now we are ready to define the phase_kernel to carry out the instructions in the circuit diagram drawn at the beginning of this section.
[200]:
@cudaq.kernel
def phase_kernel(control_register_size: int, work_register_size: int, a: int,
N: int):
"""
Kernel to estimate the phase of the modular multiplication gate |x> U |y> = |x> |a*y mod 21> for a = 4 or 5
"""
qubits = cudaq.qvector(control_register_size + work_register_size)
control_register = qubits[0:control_register_size]
work_register = qubits[control_register_size:control_register_size +
work_register_size]
h(control_register)
if a == 4 and N == 21:
modular_exp_4_21(control_register, work_register)
if a == 5 and N == 21:
modular_exp_5_21(control_register, work_register, control_register_size)
inverse_qft(control_register)
# Measure only the control_register and not the work_register
mz(control_register)
[201]:
control_register_size = 3
work_register_size = 5
values_for_a = [4, 5]
idx = 1 # change to 1 to select 5
N = 21
shots = 15000
print(
cudaq.draw(phase_kernel, control_register_size, work_register_size,
values_for_a[idx], N))
results = cudaq.sample(phase_kernel,
control_register_size,
work_register_size,
values_for_a[idx],
N,
shots_count=shots)
print(
"Measurement results for a={} and N={} with {} qubits in the control register "
.format(values_for_a[idx], N, control_register_size))
print(results)
╭───╮ »
q0 : ┤ h ├──●────●────●───●──●────────────────────────────────────────────────»
├───┤ │ │ │ │ │ »
q1 : ┤ h ├──┼────┼────┼───┼──┼───●────●────●───●──●───●────●────●───●──●──────»
├───┤ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ »
q2 : ┤ h ├──┼────┼────┼───┼──┼───┼────┼────┼───┼──┼───┼────┼────┼───┼──┼───●──»
├───┤╭─┴─╮ │ │ │ │ ╭─┴─╮ │ │ │ │ ╭─┴─╮ │ │ │ │ ╭─┴─╮»
q3 : ┤ x ├┤ x ├──┼────┼───╳──╳─┤ x ├──┼────┼───╳──╳─┤ x ├──┼────┼───╳──╳─┤ x ├»
╰───╯╰───╯ │ │ │ │ ╰───╯ │ │ │ │ ╰───╯ │ │ │ │ ╰───╯»
q4 : ────────────┼────┼───┼──┼────────┼────┼───┼──┼────────┼────┼───┼──┼──────»
╭─┴─╮ │ │ │ ╭─┴─╮ │ │ │ ╭─┴─╮ │ │ │ »
q5 : ──────────┤ x ├──┼───┼──╳──────┤ x ├──┼───┼──╳──────┤ x ├──┼───┼──╳──────»
╰───╯ │ │ ╰───╯ │ │ ╰───╯ │ │ »
q6 : ─────────────────┼───┼────────────────┼───┼────────────────┼───┼─────────»
╭─┴─╮ │ ╭─┴─╮ │ ╭─┴─╮ │ »
q7 : ───────────────┤ x ├─╳──────────────┤ x ├─╳──────────────┤ x ├─╳─────────»
╰───╯ ╰───╯ ╰───╯ »
################################################################################
»
────────────────────────────────────────────────────────────────────────────»
»
────────────────────────────────────────────────────────────────────────────»
»
──●────●───●──●───●────●────●───●──●───●────●────●───●──●───●────●────●───●─»
│ │ │ │ ╭─┴─╮ │ │ │ │ ╭─┴─╮ │ │ │ │ ╭─┴─╮ │ │ │ »
──┼────┼───╳──╳─┤ x ├──┼────┼───╳──╳─┤ x ├──┼────┼───╳──╳─┤ x ├──┼────┼───╳─»
│ │ │ │ ╰───╯ │ │ │ │ ╰───╯ │ │ │ │ ╰───╯ │ │ │ »
──┼────┼───┼──┼────────┼────┼───┼──┼────────┼────┼───┼──┼────────┼────┼───┼─»
╭─┴─╮ │ │ │ ╭─┴─╮ │ │ │ ╭─┴─╮ │ │ │ ╭─┴─╮ │ │ »
┤ x ├──┼───┼──╳──────┤ x ├──┼───┼──╳──────┤ x ├──┼───┼──╳──────┤ x ├──┼───┼─»
╰───╯ │ │ ╰───╯ │ │ ╰───╯ │ │ ╰───╯ │ │ »
───────┼───┼────────────────┼───┼────────────────┼───┼────────────────┼───┼─»
╭─┴─╮ │ ╭─┴─╮ │ ╭─┴─╮ │ ╭─┴─╮ │ »
─────┤ x ├─╳──────────────┤ x ├─╳──────────────┤ x ├─╳──────────────┤ x ├─╳─»
╰───╯ ╰───╯ ╰───╯ ╰───╯ »
################################################################################
╭─────────────╮╭────────────╮╭───╮
───────────────────────────┤ r1(-0.7854) ├┤ r1(-1.571) ├┤ h ├
╭────────────╮╭───╮╰──────┬──────╯╰─────┬──────╯╰───╯
────────┤ r1(-1.571) ├┤ h ├───────┼─────────────●────────────
╭───╮╰─────┬──────╯╰───╯ │
─●─┤ h ├──────●───────────────────●──────────────────────────
│ ╰───╯
─╳───────────────────────────────────────────────────────────
│
─┼───────────────────────────────────────────────────────────
│
─╳───────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────
Measurement results for a=5 and N=21 with 3 qubits in the control register
{ 000:2843 010:913 111:1850 001:1935 011:1830 100:2846 101:1861 110:922 }
Determining the order from the measurement results of the phase kernel¶
The measurement results from sampling the phase_kernel can be used to estimate the phase of the operator \(U|x\rangle = ax\mod N\). We will only be interested in the most probable non-zero outcomes of the sampling. Therefore, we’ll create a function top_results to extract those values.
[202]:
def top_results(sample_results, zeros, threshold):
"""Function to output the non-zero results whose counts are above the given threshold
Returns
-------
dict[str, int]: keys are bit-strings and values are the respective counts
"""
results_dictionary = {k: v for k, v in sample_results.items()}
if zeros in results_dictionary.keys():
results_dictionary.pop(zeros)
sorted_results = {
k: v for k, v in sorted(
results_dictionary.items(), key=lambda item: item[1], reverse=True)
}
top_key = next(iter(sorted_results))
max_value = sorted_results[top_key]
top_results_dictionary = {top_key: max_value}
for key in sorted_results:
if results_dictionary[key] > min(threshold, max_value):
top_results_dictionary[key] = results_dictionary[key]
return top_results_dictionary
Let’s see how the top_results extracts the top results from the measurement results for a=4 and N=21 with 3 qubits in the control register that we computed above. One of these top result is likely to be an estimate for the phase of \(U\).
[203]:
# Example
top_results(results, '000', 750)
[203]:
{'100': 2846,
'001': 1935,
'101': 1861,
'111': 1850,
'011': 1830,
'110': 922,
'010': 913}
The algorithm for translating the phase estimate of the operator \(U|x\rangle = ax\mod N\) into the order of \(a \mod N\) involves continued fractions. The function find_order_quantum below carries out this computation. To learn more about how the phase of \(U\) relates to the period of \(a \mod N\), check out these three lectures by Scott Aaronson: lecture 19, 20,
21.
[204]:
def get_order_from_phase(phase, phase_nbits, a, N):
"""Uses continued fractions to find the order of a mod N
Parameters
----------
phase: int
Integer result from the phase estimate of U|x> = ax mod N
phase_nbits: int
Number of qubits used to estimate the phase
a: int
For this demonstration a is either 4 or 5
N: int
For this demonstration N = 21
Returns
-------
int: period of a mod N if found, otherwise returns None
"""
assert phase_nbits > 0
assert a > 0
assert N > 0
eigenphase = float(phase) / 2**(phase_nbits)
f = fractions.Fraction.from_float(eigenphase).limit_denominator(N)
if f.numerator == 1:
return None
eigenphase = float(f.numerator / f.denominator)
print('eigenphase is ', eigenphase)
coefficients_continued_fraction = list(
contfrac.continued_fraction(eigenphase))
convergents_continued_fraction = list(contfrac.convergents(eigenphase))
print('convergent sequence of fractions for this eigenphase is',
convergents_continued_fraction)
for r in convergents_continued_fraction:
print(
'using the denominators of the fractions in the convergent sequence, testing order =',
r[1])
if a**r[1] % N == 1:
print('Found order:', r[1])
return (r[1])
return None
We are now ready to combine all the elements above into a function to find the order of \(a\) \(\mod N\) and test it in the factoring algoithm.
[205]:
def find_order_quantum(a, N):
"""The quantum algorithm to find the order of a mod N, when x = 4 or x =5 and N = 21
Parameters
----------
a: int
For this demonstration a will be either 4 or 5
N: int
For this demonstration N will be 21
Returns
r: int the period if it is found, or None if no period is found
-------
"""
if (a == 4 and N == 21) or (a == 5 and N == 21):
shots = 15000
if a == 4 and N == 21:
control_register_size = 3
work_register_size = 2
if a == 5 and N == 21:
control_register_size = 5
work_register_size = 5
#cudaq.set_random_seed(123)
results = cudaq.sample(phase_kernel,
control_register_size,
work_register_size,
a,
N,
shots_count=shots)
print("Measurement results:")
print(results)
# We will want to ignore the all zero result
zero_result = ''.join(
[str(elem) for elem in [0] * control_register_size])
# We'll only consider the top results from the sampling
threshold = shots * (.1)
most_probable_bitpatterns = top_results(results, zero_result, threshold)
for key in most_probable_bitpatterns:
# Convert the key bit string into an integer
# This integer divided by 8 is an estimate for the phase
reverse_result = key[::-1]
phase = int(reverse_result, 2)
print("Trying nonzero bitpattern from the phase estimation:", key,
"=", phase)
r = get_order_from_phase(phase, control_register_size, a, N)
if r == None:
print('No period found.')
continue
return r
break
else:
print(
"A different quantum kernel is required for this choice of a and N."
)
[206]:
my_integer = 21
initial_value_to_start = 5 # Try replacing 5 with 4
quantum = True
shors_algorithm(my_integer, initial_value_to_start, quantum)
Trying a = 5
Measurement results:
{ 11010:452 11001:92 11101:47 00000:2485 01001:96 00100:131 01011:1747 00101:1654 10101:1736 00110:475 11111:23 01000:50 01101:38 01110:35 01010:420 11110:22 01111:26 00011:50 01100:120 10011:35 00010:25 00001:22 11011:1710 00111:79 11100:113 10001:14 10010:29 10100:129 10110:467 10000:2536 10111:81 11000:61 }
Trying nonzero bitpattern from the phase estimation: 10000 = 1
No period found.
Trying nonzero bitpattern from the phase estimation: 01011 = 26
eigenphase is 0.8125
convergent sequence of fractions for this eigenphase is [(0, 1), (1, 1), (4, 5), (13, 16)]
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 5
using the denominators of the fractions in the convergent sequence, testing order = 16
No period found.
Trying nonzero bitpattern from the phase estimation: 10101 = 21
eigenphase is 0.65
convergent sequence of fractions for this eigenphase is [(0, 1), (1, 1), (1, 2), (2, 3), (13, 20)]
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 2
using the denominators of the fractions in the convergent sequence, testing order = 3
using the denominators of the fractions in the convergent sequence, testing order = 20
No period found.
Trying nonzero bitpattern from the phase estimation: 11011 = 27
eigenphase is 0.8421052631578947
convergent sequence of fractions for this eigenphase is [(0, 1), (1, 1), (5, 6), (16, 19)]
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 1
using the denominators of the fractions in the convergent sequence, testing order = 6
Found order: 6
The order of a =5 is 6
Found factors of N = 21: 7 and 3
[206]:
(7, 3)
Postscript¶
Recent work of Oded Regev improves Shor’s Algorithm by reducing the number of gates needed. You can read more about it here.